Automates et analyse des langages
Nous avons utilisé Lex3 pour générer un analyseur lexical. Nous allons à présent tenter de comprendre comment ce dernier procède pour accepter les mots du langage.
Automates finis
Un automate ressemble à un graphe, et est composé d'états (représentés par des cercles), et des transitions (représentées par des flèches). Un automate fini permet de reconnaitre des chaînes de caractères possibles du langage.
Chaque transition qui mène à un état correspond à une lecture.
Notre automate débute avec un état initial, peut accepter des transitions en fonction de ce qu'il lit et de l'étiquette de la transition, et se termine dans un état final. La concaténation des différentes étiquettes du chemin parcouru dans l'automate nous donne un mot accepté par le langage de l'automate.
Dans le cas d'un langage vide, nous avons un état initial, et un état final qui ne sont reliés par aucune transition.
Théorème de Kleene4
“A language is regular iff it can be accepted by a finite automaton.”« Un langage est régulier ssi il peut être accepté par un automate fini. »Comme le théorème de Kleene nous affirme que les langages réguliers sont des langages décidés par des automates finis, nous pouvons construire un automate fini pour toute expression rationnelle.
Automates finis non déterministes
Un AFN [automate fini non déterministe] (avec transitions vides) se compose de :
- Σ : l'ensemble des symboles d'entrée, l'alphabet9.
- S : l'ensemble fini d'états.
- s0 ∈ S : l'état initial.
- F ⊆ S : l'ensemble des états finaux, ou ensemble des états d'acceptation (représentés par un double cercle).
- Δ ⊆ S x (Σ ∪ {ε}) x S : la relation de transition, ou fonction de transition, qui donne pour chaque état et pour chaque symbole de Σ ∪ {ε} l'ensemble des états suivants.
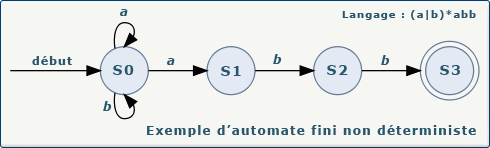
Nous pouvons remarquer que cet automate est non déterministe, car la lecture d'un caractère "a" dans l'état 0 peut mener soit à un retour à l'état 0, soit à l'état 1. Nous ne pouvons donc pas déterminer vers quel état l'automate se place après la lecture du caractère "a".
Les tables de transitions
Nous pouvons représenter nos automates sous une forme graphique, mais nous pouvons aussi les représenter sous la forme d'un tableau à deux entrées : les états et les symboles d'entrée (dans notre cas, nous avons aussi ε).
Si nous reprennons notre exemple, nous pouvons construire la table suivante :
| Symboles d'entrée | ||||
| a | b | c | ||
| États | S0 | {0,1} | {0} | ∅ |
| S1 | ∅ | {2} | ∅ | |
| S2 | ∅ | {3} | ∅ | |
| S3 | ∅ | ∅ | ∅ | |
Nous constatons que notre automate est non déterministe car nous avons plus d'une valeur pour la lecture d'un caractère a dans l'état S0.
La ligne correspondant à l'état S3 ne possède pas de valeur car nous n'avons pas de transitions depuis cet état.10
Automates finis déterministes
Lorsque nous avons un automate qui, pour chaque état et pour chaque symbole d'entrée, ne possède qu'au maximum une seule transition possible, nous n'avons plus de choix. Nous parlons alors d'automate fini déterministe [AFD].
Dans ce cas, notre AFD ne peut adopter qu'un et un seul comportement pour un mot donné
- Il ne possède pas de transition-ε
- Il ne possède qu'au maximum un état d'arrivée pour un caractère lu depuis un état de départ
Automates complets
Si nous sommes en présence d'un AFD qui possède exactement un état d'arrivée pour un caractère lu depuis un état de départ, nous parlons alors d'automate fini déterministe [AFD] complet.
Automates à pile
Si nous tentons de construire l'automate correspondant au langage non régulier12 anbn, nous ne pouvons pas assurer que le nombre de a soit identique au nombre de b.
La solution est d'utiliser une pile que nous remplissions à chaque lecture d'un caractère a et que nous dépilons ensuite à chaque lecture d'un caractère b.
Un automate à pile se compose de :
- Σ : l'ensemble des symboles d'entrée, l'alphabet.
- Q : l'ensemble fini d'états.
- q0 &isin ;Q : l'état initial.
- F ⊆ Q : l'ensemble des états finaux, ou ensemble des états d'acceptation.
- Δ fini ⊆ Q+ x (Σ ∪ {ε}) x Q* : la relation de transition.
Complémentation
Nous avons parfois besoin de créer un automate qui accepte tout ce qui n'appartient pas au langage. Cet automate est l'inverse de notre automate de départ, et nous parlons de complément.
Pour construire un automate A' qui accepte le complément de l'automate A, nous devons
- Rendre A déterministe
- Le compléter
- Ajouter un état mort
- Ajouter des transitions vers cet état
- Appliquer la propriété suivante : chaque chaîne conduit à un seul état
- inverser les états finaux et non finaux
Nederlandse vertaling
U hebt gevraagd om deze site in het Nederlands te bezoeken. Voor nu wordt alleen de interface vertaald, maar nog niet alle inhoud.Als je me wilt helpen met vertalingen, is je bijdrage welkom. Het enige dat u hoeft te doen, is u op de site registreren en mij een bericht sturen waarin u wordt gevraagd om u toe te voegen aan de groep vertalers, zodat u de gewenste pagina's kunt vertalen. Een link onderaan elke vertaalde pagina geeft aan dat u de vertaler bent en heeft een link naar uw profiel.
Bij voorbaat dank.
Document heeft de 15/05/2010 gemaakt, de laatste keer de 28/10/2018 gewijzigd
Bron van het afgedrukte document:https://www.gaudry.be/nl/langages-compilateurs-automates.html
De infobrol is een persoonlijke site waarvan de inhoud uitsluitend mijn verantwoordelijkheid is. De tekst is beschikbaar onder CreativeCommons-licentie (BY-NC-SA). Meer info op de gebruiksvoorwaarden en de auteur.
- ↑ Gnu's Not Unix : komt overeen met « GNU n'est pas UNIX » en français
- ↑ GNU : “Gnu's Not Unix” (en français, « GNU n'est pas UNIX ») Groupement de logiciels libres. Il s'agit d'un acronyme récursif, car nous retrouvons l'acronyme dans sa propre définition.
- ↑ Lex et Flex : Nous emploierons le terme Lex pour désigner l'outil d'analyse lexicale, mais il peut s'agir de Flex, son équivalant GNU
- ↑a,b Kleene : Stephen Cole Kleene, mathématicien et logicien américain, inventeur des concepts d'expression rationnelle et de langage rationnel.
- ↑ if and only if : komt overeen met « si et seulement si » en français
- ↑ ssi : si et seulement si
- ↑ AFN : automate fini non déterministe
- ↑ Transitions vides : La définition que nous utilisons ici diffère de celle de l'ouvrage de référenceref 2 car nous incluons ε dans Σ, et donc nous acceptons les transitions vides.
- ↑ S3 : Notre exemple est un exemple simple, et ne posséde pas de transition depuis l'état terminal S3, mais nous pouvons avoir des transitions au départ d'états terminaux, de même que nous pouvons avoir plus d'un état terminal dans notre automate.
- ↑ langage régulier : anbn n'est pas un langage régulier car le nombre de mots est infini et son automate n'est pas fini non plus.
Referenties

 IHDCB332 - Théorie des langages : Syntaxe et sémantique : PY Schobbens,
IHDCB332 - Théorie des langages : Syntaxe et sémantique : PY Schobbens, Syntaxe et sémantique
(January 2010)
 Compilateurs : A. Aho, M. Lam, R. Sethi, J. Ulman,
Compilateurs : A. Aho, M. Lam, R. Sethi, J. Ulman, Principes; techniques et outils
Deze verwijzingen en links verwijzen naar documenten die geraadpleegd zijn tijdens het schrijven van deze pagina, of die aanvullende informatie kunnen geven, maar de auteurs van deze bronnen kunnen niet verantwoordelijk worden gehouden voor de inhoud van deze pagina.
De auteur van deze site is als enige verantwoordelijk voor de manier waarop de verschillende concepten, en de vrijheden die met de referentiewerken worden genomen, hier worden gepresenteerd. Vergeet niet dat u meerdere broninformatie moet doorgeven om het risico op fouten te verkleinen.

