Automates et analyse des langages
Nous avons utilisé Lex3 pour générer un analyseur lexical. Nous allons à présent tenter de comprendre comment ce dernier procède pour accepter les mots du langage.
Automates finis
Un automate ressemble à un graphe, et est composé d'états (représentés par des cercles), et des transitions (représentées par des flèches). Un automate fini permet de reconnaitre des chaînes de caractères possibles du langage.
Chaque transition qui mène à un état correspond à une lecture.
Notre automate débute avec un état initial, peut accepter des transitions en fonction de ce qu'il lit et de l'étiquette de la transition, et se termine dans un état final. La concaténation des différentes étiquettes du chemin parcouru dans l'automate nous donne un mot accepté par le langage de l'automate.
Dans le cas d'un langage vide, nous avons un état initial, et un état final qui ne sont reliés par aucune transition.
Théorème de Kleene4
“A language is regular iff it can be accepted by a finite automaton.”« Un langage est régulier ssi il peut être accepté par un automate fini. »Comme le théorème de Kleene nous affirme que les langages réguliers sont des langages décidés par des automates finis, nous pouvons construire un automate fini pour toute expression rationnelle.
Automates finis non déterministes
Un AFN [automate fini non déterministe] (avec transitions vides) se compose de :
- Σ : l'ensemble des symboles d'entrée, l'alphabet9.
- S : l'ensemble fini d'états.
- s0 ∈ S : l'état initial.
- F ⊆ S : l'ensemble des états finaux, ou ensemble des états d'acceptation (représentés par un double cercle).
- Δ ⊆ S x (Σ ∪ {ε}) x S : la relation de transition, ou fonction de transition, qui donne pour chaque état et pour chaque symbole de Σ ∪ {ε} l'ensemble des états suivants.
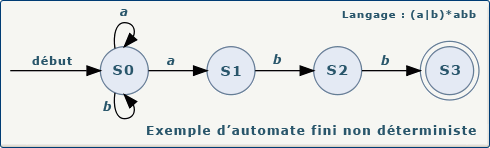
Nous pouvons remarquer que cet automate est non déterministe, car la lecture d'un caractère "a" dans l'état 0 peut mener soit à un retour à l'état 0, soit à l'état 1. Nous ne pouvons donc pas déterminer vers quel état l'automate se place après la lecture du caractère "a".
Les tables de transitions
Nous pouvons représenter nos automates sous une forme graphique, mais nous pouvons aussi les représenter sous la forme d'un tableau à deux entrées : les états et les symboles d'entrée (dans notre cas, nous avons aussi ε).
Si nous reprennons notre exemple, nous pouvons construire la table suivante :
| Symboles d'entrée | ||||
| a | b | c | ||
| États | S0 | {0,1} | {0} | ∅ |
| S1 | ∅ | {2} | ∅ | |
| S2 | ∅ | {3} | ∅ | |
| S3 | ∅ | ∅ | ∅ | |
Nous constatons que notre automate est non déterministe car nous avons plus d'une valeur pour la lecture d'un caractère a dans l'état S0.
La ligne correspondant à l'état S3 ne possède pas de valeur car nous n'avons pas de transitions depuis cet état.10
Automates finis déterministes
Lorsque nous avons un automate qui, pour chaque état et pour chaque symbole d'entrée, ne possède qu'au maximum une seule transition possible, nous n'avons plus de choix. Nous parlons alors d'automate fini déterministe [AFD].
Dans ce cas, notre AFD ne peut adopter qu'un et un seul comportement pour un mot donné
- Il ne possède pas de transition-ε
- Il ne possède qu'au maximum un état d'arrivée pour un caractère lu depuis un état de départ
Automates complets
Si nous sommes en présence d'un AFD qui possède exactement un état d'arrivée pour un caractère lu depuis un état de départ, nous parlons alors d'automate fini déterministe [AFD] complet.
Automates à pile
Si nous tentons de construire l'automate correspondant au langage non régulier12 anbn, nous ne pouvons pas assurer que le nombre de a soit identique au nombre de b.
La solution est d'utiliser une pile que nous remplissions à chaque lecture d'un caractère a et que nous dépilons ensuite à chaque lecture d'un caractère b.
Un automate à pile se compose de :
- Σ : l'ensemble des symboles d'entrée, l'alphabet.
- Q : l'ensemble fini d'états.
- q0 &isin ;Q : l'état initial.
- F ⊆ Q : l'ensemble des états finaux, ou ensemble des états d'acceptation.
- Δ fini ⊆ Q+ x (Σ ∪ {ε}) x Q* : la relation de transition.
Complémentation
Nous avons parfois besoin de créer un automate qui accepte tout ce qui n'appartient pas au langage. Cet automate est l'inverse de notre automate de départ, et nous parlons de complément.
Pour construire un automate A' qui accepte le complément de l'automate A, nous devons
- Rendre A déterministe
- Le compléter
- Ajouter un état mort
- Ajouter des transitions vers cet état
- Appliquer la propriété suivante : chaque chaîne conduit à un seul état
- inverser les états finaux et non finaux
English translation
You have asked to visit this site in English. For now, only the interface is translated, but not all the content yet.If you want to help me in translations, your contribution is welcome. All you need to do is register on the site, and send me a message asking me to add you to the group of translators, which will give you the opportunity to translate the pages you want. A link at the bottom of each translated page indicates that you are the translator, and has a link to your profile.
Thank you in advance.
Document created the 15/05/2010, last modified the 28/10/2018
Source of the printed document:https://www.gaudry.be/en/langages-compilateurs-automates.html
The infobrol is a personal site whose content is my sole responsibility. The text is available under CreativeCommons license (BY-NC-SA). More info on the terms of use and the author.
- ↑ Gnu's Not Unix : corresponds to « GNU n'est pas UNIX » en français
- ↑ GNU : “Gnu's Not Unix” (en français, « GNU n'est pas UNIX ») Groupement de logiciels libres. Il s'agit d'un acronyme récursif, car nous retrouvons l'acronyme dans sa propre définition.
- ↑ Lex et Flex : Nous emploierons le terme Lex pour désigner l'outil d'analyse lexicale, mais il peut s'agir de Flex, son équivalant GNU
- ↑a,b Kleene : Stephen Cole Kleene, mathématicien et logicien américain, inventeur des concepts d'expression rationnelle et de langage rationnel.
- ↑ if and only if : corresponds to « si et seulement si » en français
- ↑ ssi : si et seulement si
- ↑ AFN : automate fini non déterministe
- ↑ Transitions vides : La définition que nous utilisons ici diffère de celle de l'ouvrage de référenceref 2 car nous incluons ε dans Σ, et donc nous acceptons les transitions vides.
- ↑ S3 : Notre exemple est un exemple simple, et ne posséde pas de transition depuis l'état terminal S3, mais nous pouvons avoir des transitions au départ d'états terminaux, de même que nous pouvons avoir plus d'un état terminal dans notre automate.
- ↑ langage régulier : anbn n'est pas un langage régulier car le nombre de mots est infini et son automate n'est pas fini non plus.
References

 IHDCB332 - Théorie des langages : Syntaxe et sémantique : PY Schobbens,
IHDCB332 - Théorie des langages : Syntaxe et sémantique : PY Schobbens, Syntaxe et sémantique
(January 2010)
 Compilateurs : A. Aho, M. Lam, R. Sethi, J. Ulman,
Compilateurs : A. Aho, M. Lam, R. Sethi, J. Ulman, Principes; techniques et outils
These references and links indicate documents consulted during the writing of this page, or which may provide additional information, but the authors of these sources can not be held responsible for the content of this page.
The author of this site is solely responsible for the way in which the various concepts, and the freedoms that are taken with the reference works, are presented here. Remember that you must cross multiple source information to reduce the risk of errors.

