Produits de variables
Introduction: boucles simples
A . ¬B (si 4 variables)
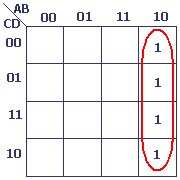
Nous ne devons pas nous occuper des variables C et D.
Regardons les valeurs pour A et B :
00, 01, 11 et 10 correspondent respectivement à ¬A . ¬B, ¬A . B, A . B et A . ¬B.
Nous pouvons donc sélectionner la colonne qui correspond à A¬B.
Produit de deux variables
Représentons les produits suivants dans un tableau de Karnaugh à 4 variables:
Produit de C et D
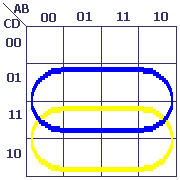
Il nous faut cerner d'une boucle toutes les cellules représentant la variable C (boucle jaune), et faire de même pour la variable D (boucle bleue).
L'intersection des deux boucles nous donne le produit de C et de D (boucle rouge).
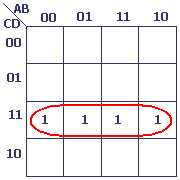
Produit de ¬A et ¬C
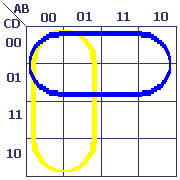
Le procédé est identique...
¬A est cerné par la boucle jaune.
¬C est cerné par la boucle bleue.
La boucle rouge représente ¬A . ¬C
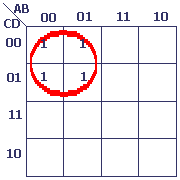
Conclusions
Le produit de deux variables correspond à un bloc de 4 cellules, de forme rectangulaire ou carrée.
Produit de trois variables
Représentons les produits suivants dans un tableau de Karnaugh à 4 variables :
Produit de A, C et D
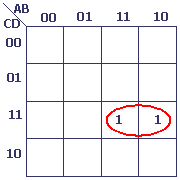
Produit de A, ¬B et D
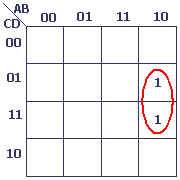
Conclusions
Le produit de trois variables correspond à un bloc de 2 cellules.
Version en cache
20/02/2025 16:04:45 Cette version de la page est en cache (à la date du 20/02/2025 16:04:45) afin d'accélérer le traitement. Vous pouvez activer le mode utilisateur dans le menu en haut pour afficher la dernère version de la page.Document créé le 19/03/2002, dernière modification le 26/10/2018
Source du document imprimé : https://www.gaudry.be//logique-produit-variables.html
L'infobrol est un site personnel dont le contenu n'engage que moi. Le texte est mis à disposition sous licence CreativeCommons(BY-NC-SA). Plus d'info sur les conditions d'utilisation et sur l'auteur.
