Graphes : matrice d'adjacence

Introduction

Nous utiliserons dans les exemples la notation définie lors de l'introduction aux graphes.

Principe de la matrice d'adjacence

$Graphes: matrice d'adjacence$

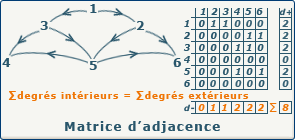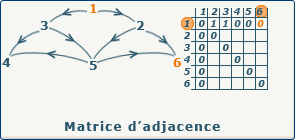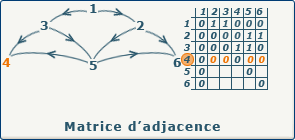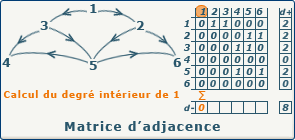
Nous pouvons représenter notre graphe G(X,A) sous la forme d'une matrice carrée de taille n*n. La ligne correspond au sommet de départ, et la colonne au sommet d'arrivée.

Ensuite, nous pouvons placer dans chaque case de notre matrice la valeur 0 ou 1 selon que le couple formé par l'indice de ligne et l'indice de colonne corresponde ou pas à un ensemble de A (en clair, 1 si l'arc existe dans le graphe). Ceci peut se traduire par la formule suivante : A_ij = 0 si (x_i,x_j)∉A, 1 si (x_i,x_j)∈A

Dans le cas d'un graphe non-orienté, notre matrice d'adjacence sera donc symétrique (x_ij=x_ji).

Nous pouvons trouver au maximum n! matrices d'adjacence pour notre graphe, selon l'ordre dans lequel nous considérons les sommets.

Algorithme de la matrice d'adjacence

Soient les matrices M, A, et B implémentées sous formes de tableaux de tableaux :

pour i variant_de 1 jusque n faire
	pour j variant_de 1 jusque n faire
		M[i,j] := 0;
		pour k variant_de 1 jusque n faire
			M[i,j] := M[i,j] &oplus; A[i,k] &otimes; B[k,j];
		fin pour
	fin pour
fin pour

Ce genre d'algorithme effectue le plus souvent le plus souvent le calcul suivant 0*0. Les deux boucles extérieures sont indispensables, mais nous pouvons par contre remplacer la boucle intérieure par les pointeurs d'arcs si ces derniers sont disponibles.

Table des matières Haut

Matrice de poids des arcs

$Matrice de poids des arcs$

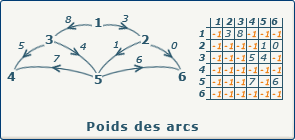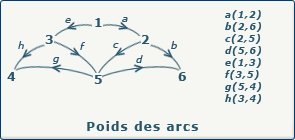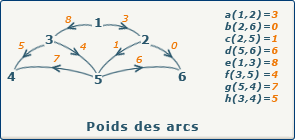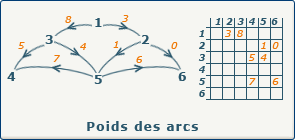
Si nous travaillons avec un graphe valué, au lieu de placer la valeur 1 quand un arc est présent, nous allons placer le poids (la valeur) de cet arc dans la case appropriée de la matrice.

Attention que dans ce cas, nous ne pouvons plus placer la valeur 0 pour signaler un arc inexistant, car cela représenterait un arc existant, de poids 0. Nous allons donc choisir arbitrairement une valeur non utilisée (par exemple -1 si nous avons la certitude que toutes nos valeurs sont positives).

Version en cache

20/12/2024 19:57:29 Cette version de la page est en cache (à la date du 20/12/2024 19:57:29) afin d'accélérer le traitement. Vous pouvez activer le mode utilisateur dans le menu en haut pour afficher la dernère version de la page.

Document créé le 11/11/2009, dernière modification le 26/10/2018
Source du document imprimé : https://www.gaudry.be/graphes-matrice-adjacence.html

L'infobrol est un site personnel dont le contenu n'engage que moi. Le texte est mis à disposition sous licence CreativeCommons(BY-NC-SA). Plus d'info sur les conditions d'utilisation et sur l'auteur.

Références

INFOB321 - Théorie des graphes : JP Leclercq, Cours de Théorie des Graphes et réseaux de Petri (September 2008)

Ces références et liens indiquent des documents consultés lors de la rédaction de cette page, ou qui peuvent apporter un complément d'information, mais les auteurs de ces sources ne peuvent être tenus responsables du contenu de cette page.
L'auteur de ce site est seul responsable de la manière dont sont présentés ici les différents concepts, et des libertés qui sont prises avec les ouvrages de référence. N'oubliez pas que vous devez croiser les informations de sources multiples afin de diminuer les risques d'erreurs.

Table des matières Haut