Graphes et arbres

Arbre

Un arbre est un graphe simplement connexe, non orienté, sans cycles (et donc forcément sans boucles¹), dans lequel nous ne pouvons retrouver qu'une seule chaîne pour relier deux sommets distincts.

Le graphe d'un arbre comporte toujours exactement n-1 arêtes².

Racine d'un graphe

La racine r dans le cas d'un graphe orienté est le sommet à partir duquel nous pouvons accéder à chaque autre sommet du graphe : ∀ y : M[r,y]=1. Ce sommet (racine) est dit ascendant à tout autre sommet.

Arborescence

Nous appelons arborescence un graphe orienté qui possède une racine et pour lequel nous avons pour chaque sommet un seul chemin depuis la racine.

Arbre et arborescence

Les concepts d'arbre et d'arborescence ne sont pas figés. Dans certains cas nous aurons besoin de passer d'une notion à l'autre.

Nous pouvons orienter un arbre à partir d'un sommet. Dans ce cas nous pouvons avoir une arborescence.

Nous pouvons considérer une arborescence comme un graphe non orienté, et dans ce cas nous avons un arbre.

Lorsque nous ne pouvons ajouter une arête ou un arc d'un graphe à un de ses sous-graphes sans perdre le caractère d'arbre ou d'arborescence, nous pouvons dire que le sous-graphe est un arbre maximal ou une arborescence maximale.

Forêt

Lorsque nous avons un graphe composé d'arbres, nous parlons de forêt. Comme un arbre peut généralement être décomposé en sous-arbres, nous avons généralement une forêt dès que nous avons un arbre dans notre graphe.

Exercice

Voici quelques graphes, à vous de déterminer si nous sommes en présence d'un arbre, d'une arborescence, d'une forêt...

Graphes | Arbre | Arborescence | Forêt |

$graphe 1$ |

oui

$graphe 2$ |

oui

non
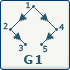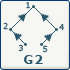L'orientation de G2 ne nous permet pas de déterminer une racine.

oui

$graphe 3$ |

non
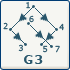Par contre nous avons 2 arbres constituées par les sous graphes {1,2,3,4,5} et {6,7}

non
Par contre nous avons 2 arborescences constituées par les sous graphes {1,2,3,4,5} et {6,7}

oui

$graphe 4$ |

non
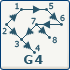Nous sommes en présence d'un cycle.

non
Il existe par exemple plusieurs chemins depuis 2 vers 3

non

$graphe 5$ |

non
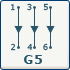Par contre nous avons 3 arbres constituées par les sous graphes {1,2}, {3,4} et {5,6}

non
Par contre nous avons 3 arborescences constituées par les sous graphes {1,2}, {3,4} et {5,6}

oui

$graphe 6$ |

oui

non
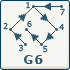L'orientation de G6 ne nous permet pas de déterminer une racine.

oui

Version en cache

22/12/2024 04:48:03 Cette version de la page est en cache (à la date du 22/12/2024 04:48:03) afin d'accélérer le traitement. Vous pouvez activer le mode utilisateur dans le menu en haut pour afficher la dernère version de la page.

Document créé le 22/11/2009, dernière modification le 09/03/2020
Source du document imprimé : https://www.gaudry.be/graphes-arbres.html

L'infobrol est un site personnel dont le contenu n'engage que moi. Le texte est mis à disposition sous licence CreativeCommons(BY-NC-SA). Plus d'info sur les conditions d'utilisation et sur l'auteur.

Notes

↑ Cycles et boucles : Une boucle correspond à la description d'un cycle (sauf que dans le cas d'une boucle le circuit ne comporte qu'un seul sommet)
↑ n : Rappel : n est la cardinalité de l'ensemble des sommets.

Table des matières Haut

Références

Arbres : lien interne, Les arbres en programmation.
INFOB321 - Théorie des graphes : JP Leclercq, Cours de Théorie des Graphes et réseaux de Petri (September 2008)

Ces références et liens indiquent des documents consultés lors de la rédaction de cette page, ou qui peuvent apporter un complément d'information, mais les auteurs de ces sources ne peuvent être tenus responsables du contenu de cette page.
L'auteur de ce site est seul responsable de la manière dont sont présentés ici les différents concepts, et des libertés qui sont prises avec les ouvrages de référence. N'oubliez pas que vous devez croiser les informations de sources multiples afin de diminuer les risques d'erreurs.

Table des matières Haut