Exemple d'algorithme de Bellman-Kalaba
Légende & situation
Le tableau de départ contient les sommets suivants :
- "Sommet 2" à l'indice 0.
- "Sommet 4" à l'indice 1.
- "Sommet 6" à l'indice 2.
- "Sommet 5" à l'indice 3.
- "Sommet 1" à l'indice 4.
- "Sommet 3" à l'indice 5.

[Étape 0-0] Initialisation des valeurs
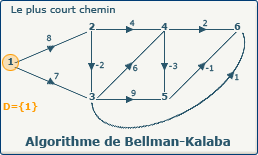
Les variables utilisées ici les mêmes que lors des explications sur l'algorithme Bellman-Kalaba, sauf pour le tableau definedVertices qui est réduit dans les images à la lettre D :
- k := arrayFirstIndex // Le compteur pointe sur le premier élément d'un tableau.
- definedVertices[k] := indice_de_la_racine //la racine fait d'office partie du chemin, car elle est le point de départ. Nous pouvons donc stocker au premier emplacement de definedVertices l'indice (dans X) du sommet.
- pathMinWeights[definedVertices[k]] := 0 // Le chemin de la racine vers la racine a un poids égal à zéro.
- verticesLabels[definedVertices[k]] := arrayFirstIndex]-1 // Étiquette de la racine. Pointe vers un emplacement non valide car la racine n'a pas de précédent.
Recherche du 1e sommet pour le chemin optimum
[Étape 1-0] Rejet du sommet 3
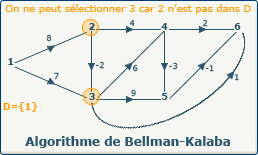
Les sommets candidats au chemin optimum sont {2,3}. Nous ne pouvons sélectionner le sommet 3 car le sommet 2 précédent de 3 n'est pas présent dans definedVertices, ce qui signifie qu'il existe un chemin non traité qui passe par le sommet 2.
i := choisir x ∈ {3 | (3 ∈ X\definedVertices) ∧ (Γ-1(3) ⊂ definedVertices ≠ ∅)};
[Étape 1-1] Sélection du sommet 2
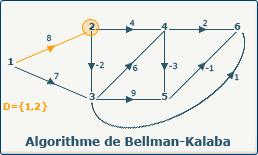
definedVertices[k] := i; devient definedVertices[0] := 0; et X[0] = sommet 2.
Le sommet 2 est sélectionné pour le chemin optimum.
Recherche du 2e sommet pour le chemin optimum
[Étape 2-0] Rejet du sommet 4
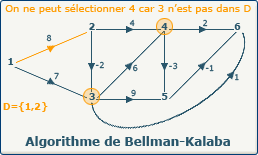
Les sommets candidats au chemin optimum sont {4,3}. Nous ne pouvons sélectionner le sommet 4 car le sommet 3 précédent de 4 n'est pas présent dans definedVertices, ce qui signifie qu'il existe un chemin non traité qui passe par le sommet 3.
i := choisir x ∈ {4 | (4 ∈ X\definedVertices) ∧ (Γ-1(4) ⊂ definedVertices ≠ ∅)};
[Étape 2-1] Sélection du sommet 3
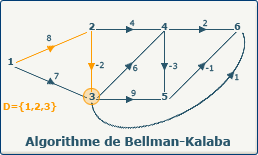
definedVertices[k] := i; devient definedVertices[0] := 5; et X[5] = sommet 3.
Le sommet 3 est sélectionné pour le chemin optimum.
Recherche du 3e sommet pour le chemin optimum
[Étape 3-0] Rejet du sommet 6
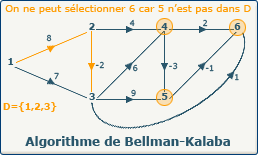
Les sommets candidats au chemin optimum sont {4,5,6}. Nous ne pouvons sélectionner le sommet 6 car le sommet 5 précédent de 6 n'est pas présent dans definedVertices, ce qui signifie qu'il existe un chemin non traité qui passe par le sommet 5.
i := choisir x ∈ {6 | (6 ∈ X\definedVertices) ∧ (Γ-1(6) ⊂ definedVertices ≠ ∅)};
[Étape 3-1] Recherche du minimum entre {4 (avec un poids de 6),5 (avec un poids de 9)}
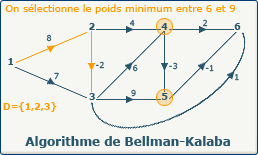
Les sommets candidats au chemin optimum sont {4 (avec un poids de 6),5 (avec un poids de 9)} Nous devons sélectionner le sommet 4 car il possède le poids le moins élevé (6) parmi les candidats.
pathMinWeights[i] := minimum{ pathMinWeigths[j]+weight(j,i)∀j∈&Gamma-1(x)};
[Étape 3-2] Sélection du sommet 4
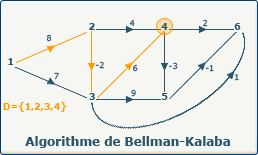
definedVertices[k] := i; devient definedVertices[0] := 1; et X[1] = sommet 4.
Le sommet 4 est sélectionné pour le chemin optimum.
Recherche du 4e sommet pour le chemin optimum
[Étape 4-0] Rejet du sommet 6
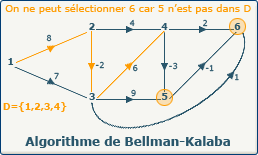
Les sommets candidats au chemin optimum sont {5,6}. Nous ne pouvons sélectionner le sommet 6 car le sommet 5 précédent de 6 n'est pas présent dans definedVertices, ce qui signifie qu'il existe un chemin non traité qui passe par le sommet 5.
i := choisir x ∈ {6 | (6 ∈ X\definedVertices) ∧ (Γ-1(6) ⊂ definedVertices ≠ ∅)};
[Étape 4-1] Sélection du sommet 5
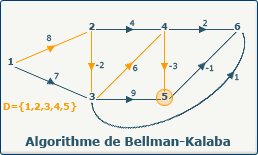
definedVertices[k] := i; devient definedVertices[0] := 3; et X[3] = sommet 5.
Le sommet 5 est sélectionné pour le chemin optimum.
Dernier sommet pour le chemin optimum (arrivée)
[Étape 5-0] Sélection du sommet 6
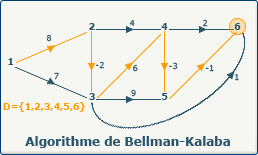
definedVertices[k] := i; devient definedVertices[0] := 2; et X[2] = sommet 6.
Le sommet 6 est sélectionné pour le chemin optimum.
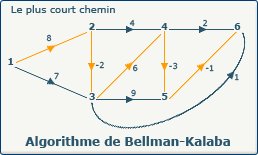
Chemin optimum trouvé par l'algorithme de Bellman-Kalaba
Version en cache
04/10/2025 14:27:12 Cette version de la page est en cache (à la date du 04/10/2025 14:27:12) afin d'accélérer le traitement.Vous pouvez activer le mode utilisateur dans le menu en haut pour afficher la version plus récente de la page.
Document créé le 26/12/2009, dernière modification le 16/07/2024
Source du document imprimé : https://www.gaudry.be/graphes-bellman-kalaba-exemple.html
L'infobrol est un site personnel dont le contenu n'engage que moi. Le texte est mis à disposition sous licence CreativeCommons(BY-NC-SA). Plus d'info sur les conditions d'utilisation et sur l'auteur.
Références
Ces références et liens indiquent des documents consultés lors de la rédaction de cette page, ou qui peuvent apporter un complément d'information, mais les auteurs de ces sources ne peuvent être tenus responsables du contenu de cette page.
L'auteur de ce site est seul responsable de la manière dont sont présentés ici les différents concepts, et des libertés qui sont prises avec les ouvrages de référence. N'oubliez pas que vous devez croiser les informations de sources multiples afin de diminuer les risques d'erreurs.




