Graphes : matrice d'adjacence

Introduction

Nous utiliserons dans les exemples la notation définie lors de l'introduction aux graphes.

Principe de la matrice d'adjacence

$Graphes: matrice d'adjacence$

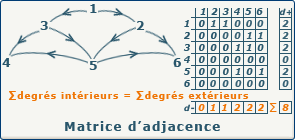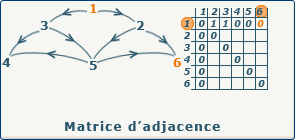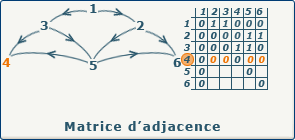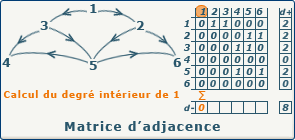
Nous pouvons représenter notre graphe G(X,A) sous la forme d'une matrice carrée de taille n*n. La ligne correspond au sommet de départ, et la colonne au sommet d'arrivée.

Ensuite, nous pouvons placer dans chaque case de notre matrice la valeur 0 ou 1 selon que le couple formé par l'indice de ligne et l'indice de colonne corresponde ou pas à un ensemble de A (en clair, 1 si l'arc existe dans le graphe). Ceci peut se traduire par la formule suivante : A_ij = 0 si (x_i,x_j)∉A, 1 si (x_i,x_j)∈A

Dans le cas d'un graphe non-orienté, notre matrice d'adjacence sera donc symétrique (x_ij=x_ji).

Nous pouvons trouver au maximum n! matrices d'adjacence pour notre graphe, selon l'ordre dans lequel nous considérons les sommets.

Algorithme de la matrice d'adjacence

Soient les matrices M, A, et B implémentées sous formes de tableaux de tableaux :

pour i variant_de 1 jusque n faire
	pour j variant_de 1 jusque n faire
		M[i,j] := 0;
		pour k variant_de 1 jusque n faire
			M[i,j] := M[i,j] &oplus; A[i,k] &otimes; B[k,j];
		fin pour
	fin pour
fin pour

Ce genre d'algorithme effectue le plus souvent le plus souvent le calcul suivant 0*0. Les deux boucles extérieures sont indispensables, mais nous pouvons par contre remplacer la boucle intérieure par les pointeurs d'arcs si ces derniers sont disponibles.

Inhaltsverzeichnis Haut

Matrice de poids des arcs

$Matrice de poids des arcs$

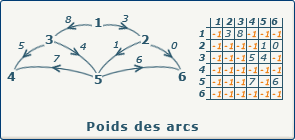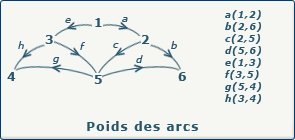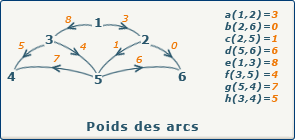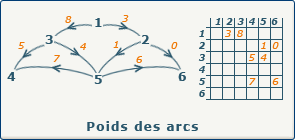
Si nous travaillons avec un graphe valué, au lieu de placer la valeur 1 quand un arc est présent, nous allons placer le poids (la valeur) de cet arc dans la case appropriée de la matrice.

Attention que dans ce cas, nous ne pouvons plus placer la valeur 0 pour signaler un arc inexistant, car cela représenterait un arc existant, de poids 0. Nous allons donc choisir arbitrairement une valeur non utilisée (par exemple -1 si nous avons la certitude que toutes nos valeurs sont positives).

Deutsche Übersetzung

Sie haben gebeten, diese Seite auf Deutsch zu besuchen. Momentan ist nur die Oberfläche übersetzt, aber noch nicht der gesamte Inhalt.

Wenn Sie mir bei Übersetzungen helfen wollen, ist Ihr Beitrag willkommen. Alles, was Sie tun müssen, ist, sich auf der Website zu registrieren und mir eine Nachricht zu schicken, in der Sie gebeten werden, Sie der Gruppe der Übersetzer hinzuzufügen, die Ihnen die Möglichkeit gibt, die gewünschten Seiten zu übersetzen. Ein Link am Ende jeder übersetzten Seite zeigt an, dass Sie der Übersetzer sind und einen Link zu Ihrem Profil haben.

Vielen Dank im Voraus.

Dokument erstellt 11/11/2009, zuletzt geändert 26/10/2018
Quelle des gedruckten Dokuments:https://www.gaudry.be/de/graphes-matrice-adjacence.html

Die Infobro ist eine persönliche Seite, deren Inhalt in meiner alleinigen Verantwortung liegt. Der Text ist unter der CreativeCommons-Lizenz (BY-NC-SA) verfügbar. Weitere Informationen auf die Nutzungsbedingungen und dem Autor.

Referenzen

INFOB321 - Théorie des graphes : JP Leclercq, Cours de Théorie des Graphes et réseaux de Petri (September 2008)

Diese Verweise und Links verweisen auf Dokumente, die während des Schreibens dieser Seite konsultiert wurden, oder die zusätzliche Informationen liefern können, aber die Autoren dieser Quellen können nicht für den Inhalt dieser Seite verantwortlich gemacht werden.
Der Autor Diese Website ist allein dafür verantwortlich, wie die verschiedenen Konzepte und Freiheiten, die mit den Nachschlagewerken gemacht werden, hier dargestellt werden. Denken Sie daran, dass Sie mehrere Quellinformationen austauschen müssen, um das Risiko von Fehlern zu reduzieren.

Inhaltsverzeichnis Haut