Demi additionneur binaire (half-adder)
Introduction
L'addition et la soustraction sont deux opérations arithmétiques de base. Nous allons donc tenter de comprendre comment l'ordinateur peut effectuer une addition.
En base 2, l'addition de deux bits correspond à ceci:
- 0 + 0 = 00
- 0 + 1 = 01
- 1 + 0 = 01
- 1 + 1 = 10
Décomposition du principe d'addition
Nous pouvons comparer cette addition avec une addition décimale, dans la mesure où il est possible d'avoir un report; rappelons nous l'addition des chiffres 5 et 6 en calcul écrit en base 10:
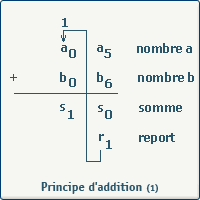
A partir du moment où un report intervient, nous devons envisager qu'il existe pour toute addition un report en entrée, et un report en sortie.
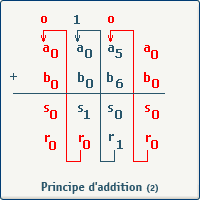
Le premier et le dernier report (en rouge dans le schéma) ont donc la valeur zéro. Il nous suffira donc d'initialiser le premier report à zéro; et le dernier report nous indiquera, dans le cas où il sera différent de zéro, qu'il y a dépassement de capacité (overflow).
Ceci nous permet de découper une addition complexe en une séquence utilisant à chaque fois le même traitement, ce que nous détaillerons dans la partie électronique.
L'addition des deux bits de bas poids (LSB: Least Significant Bit) a0 et b0, donne un résultat partiel s0 et une retenue r0. On forme ensuite la somme des deux bits a1 et b1 et de la retenue r0. Nous obtenons un résultat partiel s1 et une retenue r1. Et ainsi de suite, nous obtenons un résultat sur quatre bits S et une retenue r3.
Principe d'addition binaire: résumé
La figure suivante montre la décomposition de l'addition de deux nombres binaires de quatre bits.
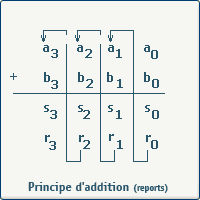
Schéma et table de vérité
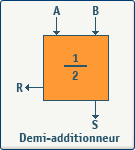
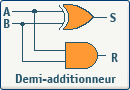
En entrée, nous avons les deux nombres à additionner (A et B), et en sortie, La somme (S) et le report (R). Ce module se nomme demi additionneur (half-adder), et nous pouvons constater qu'il ne tient pas compte du report d'entrée. Voyons donc la table de vérité :
Nous pouvons tirer certaines conclusions de cette table de vérité:
- S = A . B + A . B= A Å B
- R = A . B
Circuit logique du demi additionneur
English translation
You have asked to visit this site in English. For now, only the interface is translated, but not all the content yet.If you want to help me in translations, your contribution is welcome. All you need to do is register on the site, and send me a message asking me to add you to the group of translators, which will give you the opportunity to translate the pages you want. A link at the bottom of each translated page indicates that you are the translator, and has a link to your profile.
Thank you in advance.
Document created the 19/03/2002, last modified the 26/10/2018
Source of the printed document:https://www.gaudry.be/en/logique-half-adder.html
The infobrol is a personal site whose content is my sole responsibility. The text is available under CreativeCommons license (BY-NC-SA). More info on the terms of use and the author.
References
These references and links indicate documents consulted during the writing of this page, or which may provide additional information, but the authors of these sources can not be held responsible for the content of this page.
The author of this site is solely responsible for the way in which the various concepts, and the freedoms that are taken with the reference works, are presented here. Remember that you must cross multiple source information to reduce the risk of errors.



