Grammaires
Symbole terminal et non terminal
Nous évoquerons souvent les notions de « terminal » et de « non terminal », qui se définissent de la manière suivante :
- symboles terminaux : chaînes de caractères issues du langage (les mots).
- symboles non terminaux : ce sont les noms que nous donnons aux règles de productions pour les reconnaître. Ces symboles n'appartiennent pas au langage défini par la grammaire.
Conventions d'écriture
Au long des exemples suivants, nous tenterons de respecter les convensions suivantes1 :
- les symboles non terminaux sont représentés par des lettres majuscules du début de l'alphabet (A, B, C, ...). Ils peuvent être représentés par des mots composés de minuscules, et dans ce cas nous les entourerons par les signes plus petit et plus grand de cette manière : <non-terminal>.
- les symboles terminaux sont représentés par des lettres minuscules de la fin de l'alphabet (... x, y, z).
- les suites de symboles grammaticaux sont représentés par des lettres du début de l'alphabet grec (α (alpha), β (beta), γ (gamma), ...).
- la chaîne vide est représentés par la lettre grecque ε (epsilon).
Grammaires récursive à gauche
Une grammaire est récursive à gauche si un symbole non terminal A se dérive strictement en une proto-phrase2 commençant par A ⇒+ Aα tel que α ne commence pas par A.
Structure des grammaires
Une grammaire est composée de quatre éléments :
- VN : l'ensemble fini des symboles non-terminaux, que nous retrouvons parfois simplement sous la lettre N.
- VT : l'ensemble fini des symboles terminaux (le vocabulaire terminal)3. Cet ensemble VT est disjoint de VN.
- P : l'ensemble des productions. Il s'agit de l'ensemble des règles grammaticales.
- S : le symbole de départ (S ∈ VN).
Classes de grammaires selon Chomsky5
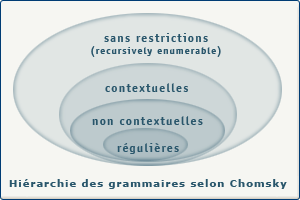
Grammaires libres6 (Type 0)
Les productions de la grammaire de type 0 sont de la forme : α → β avec α ∈ {VN ∪ VT}+ et β ∈ {VN ∪ VT}*
Ces grammaires engendrent des « langages récursivement énumérables » (en anglais, “recursively enumerable languages”), acceptés par une machine de Turing8.
Grammaires contextuelles (Type 1)
Les productions de la grammaire contextuelle sont de la forme : αΑβ → αγβ avec Α ∈ N, α, β ∈ (N ∪ Σ)* etγ ∈ (N ∪ Σ)+
Nous avons un élément non terminal (Α) qui dépend du contexte constitué par les mots qui l'encadrent (α et β).
Nous pouvons aussi accepter dans les grammaires de type 1 les productions de la forme : α → β avec α ∈ {VN ∪ VT}+ et β ∈ {VN ∪ VT}* et |α| ≤ |β|, car ces grammaires produisent des langages contextuels.
Grammaires non contextuelles9 (Type 2)
Les productions de la grammaire non contextuelle sont de la forme : A → α avec A ∈ VN et α ∈ {VN ∪ VT}*
Chomsky5 a utilisé le terme “non contextuel” (en français, « context-free ») par opposition aux “contextuel” (en français, « context-sensitive ») pour lesquelles l'application d'une règle est soumise à des conditions.
Un langage « non contextuel »10 peut être représenté par un automate à pile non déterministe. Pour prouver qu'un langage n'est pas « non contextuel »10, nous devons donc prouver qu'il n'est pas possible de construire son automate à pile.
Grammaires régulières12 (Type 3)
Les productions de la grammaire de type régulière sont de la forme :
A → α | A → αB | A → ε (grammaire linéaire à droite13) ou A → α | A → Bα | A → ε (grammaire linéaire à gauche14)
avec A ∈ VN et α ∈ {VN ∪ VT}*
Un langage est régulier ssi un programme peut le lire (de gauche à droite) en ne mémorisant qu'une information finie.
Nous pouvons définir un langage régulier de la manière suivante :
- Soit Σ l'alphabet (fini) du langage L
- ∅ est un langage régulier;
- {ε} est un langage régulier;
- ∀ a ∈ Σ, {a} est un langage régulier (langages de mots à une seule lettre);
- si L1 et L2 sont réguliers, alors
- L1L2 = {W1W2 | W1 ∈ L1, W2 ∈ L2} est régulier
- L1 ∪ L2 est régulier
- L* = {ε} ∪ {wwww...w | W ∈ L} est régulier
Pour prouver qu'un langage est régulier, nous pouvons soit donner l'expression rationelle qui correspond, soit donner son AFN [automate fini non déterministe].
Pour prouver qu'un langage n'est pas régulier, nous pouvons soit montrer que nous ne pouvons construire son AFN, soit utiliser le lemme de pompage17.
Tout langage fini est un langage régulier. Un langage non fini peut toutefois être un langage régulier si son automate est fini et contient un cycle.
Tout langage régulier est un langage « non contextuel »10.
Certaines grammaires non régulières peuvent tout de même engendrer des langages réguliers.
Grammaires LL(k)
- Le premier L signifie “Left to right scanning” (en français, « parcours de la gauche vers la droite »)
- Le second L signifie “Leftmost derivation” (en français, « dérivation gauche »)
- La lettre k est remplacé par un nombre qui signifie que le choix de la bonne expansion doit pouvoir se faire sur la base des k prochains symboles à lire.
Une grammaire récursive à gauche n'est jamais une grammaire LL(k).
Grammaires LL(1)
Les grammaires LL(1) sont généralement suffisantes pour la construction de langages de programmation, pour peu qu'ils respectent les conditions qui suivent.
Une grammaire G est LL(1) ssi pour toute paire de productions distinctes Α → α | β de G :
- Il n'existe aucun symbole terminal a tel que α et β dérivent tous deux des chaînes commençant par a.
- Les chaînes α et β ne peuvent dériver toutes deux la chaîne vide.
- Si β ⇒* ε, alors α ne dérive aucune chaîne commençant par un terminal qui est dans SUIVANT(A).
De même, si α ⇒* ε, alors β ne dérive aucune chaîne commençant par un terminal qui est dans SUIVANT(A).
Comment rendre une grammaire LL(1) ?
- Eliminer la récursivité gauche.
Par exemple, A ::= Aα | β devient A ::= βA', A' ::= αA' | ε (nous avons alors une récursivité droite) - Factoriser les parties communes (nous postposons le choix en groupant les parties communes).
Par exemple, I ::= if E then I | if E then I else I devient I ::= if E then I C et C ::= ε | else I.
Grammaires ambiguës
Si nous pouvons générer plus d'un arbre syntaxique pour une même chaîne du langage, nous pouvons dire que la grammaire est ambiguë.
Nous pouvons être confrontés à des grammaires ambiguës quand par exemple α et β sont ε-productifs.
Nous pouvons généralement résoudre engendrés par une grammaire ambiguë en définissant des règles de précédence ou d'associativité.
Grammaires LR(k)
- Le premier L signifie “Left to right scanning” (en français, « parcours de la gauche vers la droite »)
- Le second R signifie “Rightmost derivation” (en français, « dérivation droite »)
- La lettre k est remplacé par un nombre qui signifie que le choix de la bonne expansion doit pouvoir se faire sur la base des k symboles anticipés et non consommés.
Un analyseur LR(k) effecute une analyse ascendante sur les grammaires non contextuelles.
Nous retrouvons souvent simplement le terme LR, pour lequel LR(1) est sous-entendu.
Grammaires LR(0)
Un analyseur LR(k) n'effectue aucune anticipation pour décider quelle réduction il doit entreprendre. Si nous constatons que la table des actions contient plus d'une action dans une même cellule, nous avons la certitude que lq grammaire n'est pas LR(0), et nous devons alors augmenter le nombre de symboles de prévision.
Grammaires SLR
Les analyseurs SLR(0) est utilise un autre algorithme d'analyse descendante, version renforcée de LR(0).
Afin de résoudre les conflits LR(0), nous devons alors consulter SUIVANT(A), où A est le côté gauche de la règle à réduire.
Grammaires LALR
Un automate à pile permet d'analyser une grammaire LALR [“Look-Ahead Left Recursive”21]. Un exemple célèbre d'analyseur syntaxique LALR est YACC.
Grammaires attribuées
Les grammaires attribuées sont des grammaires non contextuelles étendues avec des attributs (typage, table des symboles, etc.) associés à des valeurs, et définis par des règles d'attribution associées aux productions (les règles de la grammaire).
Lemme de pompage
Si le nombre d'états de l'automate est plus petit que la chaîne, la chaîne contient une boucle qui peut être répetée. Nous pouvons alors dire que la partie de la boucle est « pompée ».
Lemme de pompage des langages réguliers12
Nous utiliserons par la suite la décomposition que nous permet le lemme de pompage pour prouver par l'absurde qu'un langage n'est pas régulier.
Si le langage est régulier, nous pouvons le décomposer selon la formule qui suit.
- Soit L un langage sur un alphabet Σ.
Si L est régulier alors∃ p ∈ N : ∀ w ∈ L, |w| ≥ p ⇒ ∃ x,y,z Σ* :- w = xyz
- |y| ≥ 1
- |xy| ≤ p
- ∀ n ∈ N, x yn z ∈ L
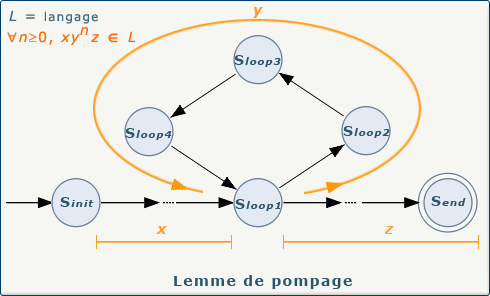
Le lemme de pompage indique que nous pouvons répéter une partie centrale du mot, et que le mot ainsi produit appartient toujours au langage décrit : ∀ n ≥ 0, xynz ∈ L
Notre automate est dans son état initial (Sinit). Nous pouvons accepter une séquence de caractères (partie x) qui nous fait passer d'état en état jusqu'au moment où l'acceptation du caractère lu nous placera dans le premier état de la boucle (partie y). Ensuite nous pouvons passer par un certain nombre d'états (partie z).
Exemple : le langage qui comprend les nombres pairs en binaire (0, 10, 100, 110, etc.).
Nous représentons donc les nombres pairs en binaire par un 0, ou un 1 suivi d'un certain nombre de 0 ou de 1, et enfin un 0 pour terminer.
L'expression rationnelle qui correspond à ce langage est 0|1(0|1)*0, ce qui correspond parfaitement au lemme de pompage (x y* z) avec :
- x = 1
- y = (0|1)*
- z = 0
Lemme de pompage des langages non contextuels
- Soit L un langage sur un alphabet Σ.
Si L est « non contextuel »10 alors∃ p ∈ N : ∀ s ∈ L, |s| ≥ p ⇒ ∃ x,y,z,v,w Σ* :- s = xvywz
- |vw| ≥ 1
- |vyw| ≤ p
- ∀ n ∈ N, x vn y wn z ∈ L
ε-productif
Nous pouvons parler de symbole non terminal ε-productif si ce non terminal A ∈ VN et que A ⇒ *ε
Table des analyseurs et des langages
| Type | Direction | Dérivation | Info |
| LL(k) | analyse descendante | gauche | choix de la bonne expansion sur les k prochains symboles à lire |
| LL(1) | analyse descendante | gauche | pour chaque non terminal, chaque production commence par un symbole terminal différent |
| LR(k) | analyse asscendante | droite | la production est déterminée après lecture du texte correspondant. |
| SLR(k) | analyse asscendante | droite | Utilisation d'un symbole de prévision. |
| LALR | analyse asscendante | droite | Union des états de même cœur parmi les éléments LR(1). |
| Type | Langage | Automate | Info |
| type 00 | récursivement énumérable | machine de Turing | |
| type 01 | récursif | machine de Turing totale | Ne fait pas partie de la hiérarchie de Comsky. |
| type 10 | contextuel | machine de Turing | |
| type 11 | indexé | automate à piles imbriquées | Ne fait pas partie de la hiérarchie de Comsky. La pile de l'automate peut contenir pour chaque entrée une donnée ou une pile (Nested stack). |
| type 12 | semi contextuel | EPDA | Ne fait pas partie de la hiérarchie de Comsky. La pile de l'automate est une pile de piles (Embedded pushdown automaton). |
| type 20 | non contextuel | automate à pile non déterministe | |
| type 21 | non contextuel déterministe | automate à pile déterministe | Ne fait pas partie de la hiérarchie de Comsky. |
| type 22 | à mots imbriqués | automate pour mots imbriqués | Ne fait pas partie de la hiérarchie de Comsky. |
| type 30 | rationnel | automate fini |
|
| type 31 | Star free | automate pour mots imbriqués | Ne fait pas partie de la hiérarchie de Comsky. Langage rationnel dont l'expression rationnelle n'emploie pas l'étoile de Kleene. |
Version en cache
04/10/2025 15:52:40 Cette version de la page est en cache (à la date du 04/10/2025 15:52:40) afin d'accélérer le traitement.Vous pouvez activer le mode utilisateur dans le menu en haut pour afficher la version plus récente de la page.
Document créé le 16/05/2010, dernière modification le 28/10/2018
Source du document imprimé : https://www.gaudry.be/langages-grammaires.html
L'infobrol est un site personnel dont le contenu n'engage que moi. Le texte est mis à disposition sous licence CreativeCommons(BY-NC-SA). Plus d'info sur les conditions d'utilisation et sur l'auteur.
- ↑ Conventions d'écriture : Ce sont les convensions utilisées dans les ouvrages qui ont servi de référence à la rédaction de ce document, mais nous pouvons trouver d'autres notations dans la litérature.
- ↑ proto-phrase : Nous parlons de « proto-phrase » pour indiquer que sa construction n'est pas achevée.
- ↑ VT : Nous utiliserons VT et non Σ, car nous sommes dans le cas d'une analyse syntaxique, et l'analyse syntaxique se base sur le résultat de l'analyse lexicale de Σ, Σ représentant l'ensemble fini qui correspond à « l'alphabet » du langage analysé.
- ↑a,b Noam Chomsky : Linguiste et philosophe américain, professeur au MIT [Massachusetts Institute of Technology]
- ↑ Grammaires libres : Nous pouvons aussi retrouver les grammaires libres sous l'appellation « grammaires générales », ou “unrestricted grammars” et “phrase structure grammar” en anglais..
- ↑ langages récursivement énumérables : correspond à “recursively enumerable languages” en anglais
- ↑ Alan Mathison Turing : Mathématicien britanique, inventeur des concepts de programmation et de programme.
- ↑ Grammaires non contextuelles : Nous pouvons aussi retrouver les grammaires non contextuelles sous l'appellation « grammaires algébriques », ou “context-free grammar” et “phrase structure grammar” en anglais..
- ↑ contextuel : correspond à « context-sensitive » en français
- ↑a,b Régulier : Le qualificatif « régulier » est souvent employé comme traduction textuelle de l'anglais “regular”, mais nous devrions bien employer « rationnel ». Cependant, nous utiliserons pour l'instant le terme « régulier » car c'est de cette manière qu'il figure dans les ouvrages de référence.
- ↑ Grammaire linéaire à droite : grammaire dont chaque membre à droite de la flèche finit par un non terminal.
- ↑ Grammaire linéaire à gauche : grammaire dont chaque membre à droite de la flèche commence par un non terminal.
- ↑ Non régulier & lemme de pompage : Nous utiliserons le lemme de pompage pour prouver que notre langage n'est pas régulier, mais nous ne pouvons pas utiliser le lemme de pompage pour prouver qu'un langage est régulier.
- ↑ Simple Left to right scanning with Rightmost derivation : correspond à « simple parcours de la gauche vers la droite avec dérivation droite » en français
- ↑ SLR(0) : “Simple Left to right scanning with Rightmost derivation” (en français, « simple parcours de la gauche vers la droite avec dérivation droite »)
- ↑a,b Look-Ahead Left Recursive : correspond à « analyseurs syntaxiques LR avec anticipation » en français
- ↑ Yet Another Compiler Compiler : correspond à « Encore un autre compilateur de compilateur » en français
- ↑ YACC : “Yet Another Compiler Compiler” (en français, « Encore un autre compilateur de compilateur »)
Références

 IHDCB332 - Théorie des langages : Syntaxe et sémantique : PY Schobbens,
IHDCB332 - Théorie des langages : Syntaxe et sémantique : PY Schobbens, Syntaxe et sémantique
(January 2010)
 Compilateurs : Dick Grune, Henry E. Bal, Ceriel J.H. Jacobs, Koen G. Langendoen,
Compilateurs : Dick Grune, Henry E. Bal, Ceriel J.H. Jacobs, Koen G. Langendoen, Cours et exercices corrigés

 Compilateurs : A. Aho, M. Lam, R. Sethi, J. Ulman,
Compilateurs : A. Aho, M. Lam, R. Sethi, J. Ulman, Principes; techniques et outils

 Structures syntaxiques : Noam Chomsky
Structures syntaxiques : Noam Chomsky
 Three models for the description of language : Noam Chomsky,
Three models for the description of language : Noam Chomsky, IRE Transactions on Information Theory
(September 1956)
 Automata theory : Wikipedia,
Automata theory : Wikipedia, formal languages and formal grammars
(version 06/05/10)
Ces références et liens indiquent des documents consultés lors de la rédaction de cette page, ou qui peuvent apporter un complément d'information, mais les auteurs de ces sources ne peuvent être tenus responsables du contenu de cette page.
L'auteur de ce site est seul responsable de la manière dont sont présentés ici les différents concepts, et des libertés qui sont prises avec les ouvrages de référence. N'oubliez pas que vous devez croiser les informations de sources multiples afin de diminuer les risques d'erreurs.

