Algorithmes gloutons

Contents

Dans notre précédente approche de la programmation dynamique, et plus précisément la partie "diviser pour régner", nous divisions le problème en une série de problèmes plus simples, jusqu'au moment où la résolution du problème devient un cas de base, simple à effectuer. Ce type d'approche nous permet généralement de résoudre d'une manière optimale nos différents problèmes, mais il existe des problèmes pour lesquels une petite augmentation de la quantité de données à traiter mène rapidement la résolution du problème hors des capacités de nos machines, tant le nombre de possibilités devient important (par exemple le problème du voyageur de commerce).

Un cas d'algorithme glouton souvent utilisé est l'allocation de ressources (scheduler¹ pour un processeur, salle de spectacle, création d'un horaire, etc.). Nous devons alors réguler l'accès aux ressources pendant un temps déterminé en respectant une série de contraintes.

Principe de l'algorithme glouton

Comme nous ne pouvons raisonnablement pas explorer toutes les solutions, nous allons procéder par choix heuristique. Comme un glouton qui cherche à avaler rapidement le plus posible, ou à réaliser le meilleur profit à court terme, nous allons présumer que le meilleur choix à court terme est le meilleur à long terme, et que l'ensemble des meilleurs choix à court terme nous ménera à une solution qui représente le meilleur choix dans sa totalité.

Nous constaterons cependant que ce n'est pas une constante, et qu'il est parfois préférable d'effectuer un choix qui semble mauvais à court terme (par exemple effectuer un investissement au lieu d'empocher un gain immédiat), mais qui conduit à un gain plus important à la fin. Pour cette raison, nous pouvons par exemple décider d'utiliser un algorithme glouton pour nous proposer rapidement une première solution qui serait de bonne qualité, et ensuite un type d'algorithme plus lent qui comparerait la solution avec d'autres. Nous utiliserons ce genre d'algorithme hybride lors de l'implémentation de paradigmes tels que "générer et tester" ou "branch and bound".

Contents Haut

L'algorithme glouton n'est pas optimal

Nous pouvons aisément démontrer que l'algorithme glouton ne nous fournit pas la meilleure solution par un contre-exemple: le problème du rendu de monnaie.

Soit e l'ensemble des monnaies. Le problème consiste à rendre une valeur s en utilisant le moins de pièces possible.

Selon le principe de l'algorithme glouton, nous utilisons le profit immédiat le plus important, donc la première pièce que nous rendons est celle qui a la plus grande valeur dans notre ensemble et dont la valeur ne dépasse pas la somme à rendre. Ensuite nous répétons l'opération sur une valeur plus simple (la somme à rendre, moins la pièce rendue) : nous avons donc un algorithme qui peut s'écrire de manière récursive.

Voici ce que cela peut donner en pseudo code :

fonction retourMonnaie(s: Entier, e: Liste<Entier>, r: Liste<Entier>)
s = somme à rendre
e = liste des monnaies possible
r = liste des monnaies déjà rendues
modifie : r
pré-condition : s: Entier initialisé ∧ e≠ {} ∧ ∀i ∈ e, j ∈ e | i=j ∧ r initialisé
post-condition : e_pre=e_post ∧ ∀ s=∑{e_i,...e_n} #x ⇒ {e_j,...e_k} #y | y<x²

Code (Pseudo-code de retourMonnaie) (7 lignes)

fonction retourMonnaie(s: Entier, e: Liste<Entier>, r: Liste<Entier>) : Liste<Entier>
si s=0
	renvoyer r
sinon
	Entier x=la plus grande valeur inférieure ou égale à s
	r = cons(x, r)
	renvoyer retourMonnaie(s-x, r)

Mauvais choix

Si nous exécutons ce code avec l'ensemble de monnaies {1, 4, 6, 7} pour nous rendre 10, il nous retourne l'ensemble de quatre pièces {7, 1, 1, 1} alors que la solution optimale est l'ensemble de deux pièces {6, 4}. Pour nous rendre 24, il nous retourne l'ensemble {7, 7, 7, 1, 1, 1} au lieu de l'ensemble {6, 6, 6, 6}

Avec l'ensemble de monnaies en euro cents {1, 2, 5, 10, 20, 50, 100, 200}, il semble nous donner toujours une solution optimale. Par exemple pour rendre 10 il retourne {10}, et pour 24 il retourne {20, 2, 2}.

Contents Haut

Critères de la stratégie gloutonne

Comme nous l'avons constaté lors de l'exemple du rendu de monnaie, le choix de l'ensemble de départ influence énormément le type de solution retournée. Nous devons veiller à avoir une sous-structure optimale, car une solution optimale d'un problème est la résolution de solutions optimales de problèmes similaires plus petits. Ce choix du sous-ensemble est un facteur qui nous indique si l'application d'un algorithme glouton à notre problème nous est bénéfique ou pas.

Un autre critère très important est le choix glouton à effectuer au niveau de notre sous-ensemble. En programmation gloutonne, nous effectuons le choix qui nous semble le plus opportun sur le moment, et puis nous résolvons les problèmes que ce choix implique. Nous élaguons³ une partie de l'arbre des solutions à chaque choix, alors que dans le cas de "diviser pour régner" le choix était fait pour chaque sous-ensemble.

English translation

You have asked to visit this site in English. For now, only the interface is translated, but not all the content yet.

If you want to help me in translations, your contribution is welcome. All you need to do is register on the site, and send me a message asking me to add you to the group of translators, which will give you the opportunity to translate the pages you want. A link at the bottom of each translated page indicates that you are the translator, and has a link to your profile.

Thank you in advance.

Document created the 19/10/2009, last modified the 16/07/2024
Source of the printed document:https://www.gaudry.be/en/programmer-algorithme-glouton.html

The infobrol is a personal site whose content is my sole responsibility. The text is available under CreativeCommons license (BY-NC-SA). More info on the terms of use and the author.

Notes

↑ Scheduler : Le scheduling (en français ordonnancement) est la répartition de tâches en fonction des ressources. Vous pouvez par exemple consulter les pages relatives à la gestion des processus par le scheduler.
↑ Post-condition : e_pre=e_post ∧ ∀ s=∑{e_i,...e_n} #x ⇒ 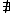{e_j,...e_k} #y | y<x signifie "Pour tout ensemble de valeurs de e entre les bornes i et n (de nombre d'éléments x) dont la somme des valeurs correspond à la somme à rendre (s), il n'existe pas d'ensemble plus petit ensemble (de nombre d'éléments y) dont la somme corresponde à s"
↑ Pruning : Le pruning (élaguage en français) est surtout utilisé en "branch and bound" pour éviter d'explorer certaines branches de l'arbre des solutions.

Contents Haut

References

IHDCB331 - Méthodes de Programmation : PY Schobbens, Cours de Méthodes de Programmation (September 2009)
Introduction to Algorithms : Thomas H. Cormen, Charles E. Leiserson, and Ronald L. Rivest (2000)

These references and links indicate documents consulted during the writing of this page, or which may provide additional information, but the authors of these sources can not be held responsible for the content of this page.
The author This site is solely responsible for the way in which the various concepts, and the freedoms that are taken with the reference works, are presented here. Remember that you must cross multiple source information to reduce the risk of errors.

Contents Haut