test
Algorithmes de tris
Dans nos différents algorithmes de tri, nous rencontrerons principalement deux types d'opérations : les comparaisons et les permutations. Il est clair que les performances des algorithmes différeront selon le nombre et la proportion de ces opérations (les comparaisons sont nettement moins coûteuses que les permutations).
Bien que ces deux types représentent les opérations fondamentales des algorithmes de tris, nous pouvons à certains moments utiliser un autre type d'opération : les affectations, pour remplacer certaines suites de permutations (une permutation est en fait une série de trois affectations).
Voyons à présent comment implémenter les différents algorithmes :
- Tri par échanges (exchange sort ou bubble sort)
- Tri par sélection (selection sort)
- Tri par insertion (insertion sort)
- Tri Shell (shell sort), amélioration du tri par insertions
- Tri par tas (heap sort)
- Tri par fusion (merge sort)
- Tri rapide (quick sort)
Exemples concrets d'implémentations : les tris en C, trier des structures en C, les tris en Java.
Bubble Sort : Tri par échanges
Comme des bulles qui remontent à la surface, les éléments de plus faibles valeurs se déplacent vers le début de notre tableau. C'est pourquoi cette technique de tri est souvent nommée le tri à bulles (bubble sort), mais nous le retrouvons aussi sous le nom de tri par échanges (exchange sort).
C'est le tri le plus simple, mais il en existe de très nombreuses variantes. Nous verrons une implémentation de base, et une petite amélioration de cette implémentation générale.
Boucle intérieure
Nous nous positionnons à la fin du tableau, et nous comparons le dernier élément (à l'index i) avec son prédécesseur (à l'index i-1). S'il est plus petit que son prédécesseur, nous permutons les deux éléments.
Ensuite, nous nous positionnons sur l'avant dernier élément (i=i-1), et nous comparons ce dernier (à l'index i) avec son prédécesseur (à l'index i-1). S'il est plus petit que son prédécesseur, nous permutons les deux éléments.
Nous répétons ces opérations jusqu'au moment où le deuxième élément du tableau est atteint.
Pourquoi ne pas aller jusqu'au premier élément ? Parceque dans ce cas, nous comparerions le premier élément avec son prédécesseur qui n'existe pas (OutOfBoundException).
A la fin de ces opérations, nous avons la certitude que le premier élément du tableau est le plus petit.
Boucle extérieure
Nous devrions normalement effectuer le travail complet de la boucle intérieure un nombre de fois égal à la taille du tableau.
extérieure | 8 | 4 | 6 | 2 | 13 | 4 | 1 | 20 |
Légende :
Valeurs de départ | Comparaisons | Permutations | Valeurs triées
Que pouvons nous remarquer ?
Les éléments sont correctement triés, mais nous avons un gaspillage à deux niveaux :
- interne : après le premier passage, il n'est plus nécessaire de comparer la première valeur, et ainsi de suite.
- externe : depuis le 5è passage de la boucle externe, les éléments sont triés.
Afin d'améliorer notre système, nous pouvons diminuer d'une unité (décrémenter) la valeur de notre compteur pour la boucle intérieure à chaque passage dans la boucle extérieure.
En plus, nous pouvons utiliser un booléen qui sera à false à chaque début de la boucle extérieure, et qui sera mis à true si une permutation a eu lieu. Si aucune permutation n'a eu lieu après une boucle intérieure, le tableau est trié.
extérieure | 8 | 4 | 6 | 2 | 13 | 4 | 1 | 20 |
Légende :
Valeurs de départ | Comparaisons | Permutations | Valeurs triées
Selection Sort : Tri par sélections
Le principe du tri par sélection est de diminuer le nombre de permutations, en le limitant au nombre d'éléments à trier. Par rapport à un tri par insertions ou un tri à bulles, le nombre de comparaisons sera ici égal ou même suppérieur. Ceci devient pourtant très intéressant dans le cas où la comparaison des éléments a un coût peu élevé, mais que les permutations ont un coût élevé (le déplacement des éléments -qui est un ensemble de suppressions et d'ajouts- dans la structure utilisée nécessite beaucoup de ressources en temps ou en mémoire).
Nous pouvons procéder de 2 manières, de la plus petite vers la plus grande valeur (du début vers la fin), ou de la plus grande vers la plus petite valeur (de la fin vers le début).
Tri par sélection de la plus petite valeur
Ce tri porte aussi le nom de tri par sélection en ordre croissant.
Nous commencons par le premier élément du tableau, que nous allons comparer avec le reste des éléments, à la recherche du plus petit. A chaque fois que nous rencontrerons un élément plus petit, celui-ci devient le candidat à la permutation.
extérieure | 8 | 4 | 6 | 2 | 13 | 4 | 1 | 20 |
Légende :
Valeurs de départ | Valeur à permuter | Comparaisons | Candidat à la permutation | Permutations | Valeurs triées
Tri par sélection de la plus grande valeur
Ce tri porte aussi le nom de tri en ordre décroissant.
Cet algorithme de tri est plus souvent utilisé. Le principe est identique, mais nous plaçons les éléments dans le tableau depuis la dernière case (qui contiendra l'élément qui possède la valeur la plus élevée) jusqu'à la première (la plus petite valeur).
Nous commencons par le dernier élément du tableau, que nous allons comparer avec le reste des éléments, à la recherche du plus grand. A chaque fois que nous rencontrerons un élément plus grand, celui-ci devient le candidat à la permutation.
extérieure | 8 | 4 | 6 | 2 | 13 | 4 | 1 | 20 |
Légende :
Valeurs de départ | Valeur à permuter | Comparaisons | Candidat à la permutation | Permutations | Valeurs triées
Comparaisons entre le tri par sélection en ordre croissant et le tri par sélection en ordre décroissant
Lorsque nous effectuons des permutations, lors du tri par sélection en ordre croissant l'ordre d'apparition des éléments égaux (la valeur 4 dans nos exemples) est préservée. L'ordre est inversé lors de tri par sélection en ordre décroissant.
Propriétés du tri par sélection
Le nombre de passages dans la boucle extérieure est identique au nombre d'éléments de notre structure. Dans le cas de notre tableau, nous pouvons légèrement optimiser le code en évitant de comparer la dernière valeur avec elle même, mais ce gain serait compensé par un test qui serait effectué à chaque passage (par exemple en vérifiant que les deux indexes de cellules sont identiques, ce qui signifie que l'on travaille sur une seule cellule et qu'il n'est pas nécessaire de la trier).
A chaque passage dans la boucle extérieure, le nombre de comparaisons diminue de 1. Au xième passage dans la boucle extérieure, nous avons x-1 comparaisons.
Complexité du tri par sélection

Exemple de code Pascal de tri par sélections
Code Pascal (Tri par sélection) (66 lignes)
Tri par insertions
Le tri par insertion permet d'éviter les nombreuses permutations du tri par échanges.
Le principe général est de comparer une valeur de référence avec toutes celles qui suivent tant que la valeur suivante est inférieure, ou jusqu'à la fin du tableau si aucune valeur ne lui est supérieure. La valeur de référence sera placée après la dernière valeur qui lui est inférieure.
Il s'agit donc de mémoriser cette valeur référence, de déplacer d'une position le bloc des éléments valeurs inférieures ou égales qui suit, puis de placer la valeur référence dans la cellule libérée.
En réalité, le déplacement du bloc consiste en une série d'affectations (t[i]=t[i+1]).
Comme nous ne pouvons comparer la dernière valeur du tableau avec ses suivantes, nous débuterons la boucle à l'avant dernière valeur du tableau, jusqu'à la première.
extérieure | 8 | 4 | 6 | 2 | 13 | 4 | 1 | 20 |
Légende :
Valeurs de départ | Valeur de référence | Comparaisons | Déplacement | Valeurs triées
Ordre de grandeur du tri par insertions
Nous pouvons appliquer le principe diviser pour régner pour le tri par insertion, même si à chaque fois nous avons un élément suivi par le reste des éléments. Ceci nous rappelle les méthodes head() et tail() que nous avions défini dans notre type abstrait Liste.
Selon le type de structure utilisé, la partie "combiner" (qui correspond àinsérer un élément) dans une liste triée est de ![]() (n), ou pour un arbre rouge-noir de
(n), ou pour un arbre rouge-noir de ![]() (log n), ce qui nous donne
(log n), ce qui nous donne ![]() (n2) pour l'exécution totale du tri par insertions.
(n2) pour l'exécution totale du tri par insertions.
Heap Sort : Tri par tas
Le heap sort est basé sur les abres binaires balancés, ou red black tree(cliquez ici pour plus d'informations sur le parcours des éléments d'un arbre).
Un arbre est composé de nœuds qui sont reliés entre eux de manière à former une structure hiérarchique, dont chaque nœud ne peut avoir qu'un seul parent. Le premier nœud se nomme la racine (root), mais la représentation des arbres est le plus souvent inverse à la nature, présentant la racine en haut, et les branches vers les enfants vers le bas. Les nœuds qui n'ont pas d'enfants sont nommés les feuilles (leaves).
Un arbre binaire est un arbre dont chaque nœud peut être parent de deux nœuds enfants maximum.
La hauteur d'un arbre correspond au nombre de nœuds composant le chemin le plus long de la racine à la feuille la plus basse.
Dans un arbre binaire balancé (équilibré), chaque niveau double le nombre de nœuds du niveau précédent (si le nombre d'éléments ne s'y prête pas, c'est seulement le dernier niveau qui ne comportera pas exactement le double du précédent).
Nous pouvons donc en déduire certaines relations :
- h = hauteur de l'arbre binaire balancé complet
- n = nombre d'éléments de l'arbre
n = 2h - 1
et
h = log2(n + 1)
Ces notions sont importantes, car nous travaillons avec une structure logique en arbre, mais avec une structure réelle en tableau.
Principe du Heap sort
Dans le cas du heap sort nous travaillerons en deux phases :
- La construction.
- Le tri.
Après chaque phase de tri, l'élément de la valeur la plus élevée se trouve repoussé en bas de l'arbre (puisque le but est d'avoir le plus petit élément en premier lieu, puis les éléments ordonnés de manière croissante). Il est donc nécessaire de reconstruire un nouvel arbre sans tenir compte de l'élément trié, et de répéter ce cycle jusqu'au moment où il ne reste plus qu'un élément.
Quick Sort : Tri rapide
Le tri rapide repose sur le principe "diviser pour régner" (divide and conquer). Nous pouvons simplifier le tri en divisant notre structure en structures plus petites (par exemple diviser notre tableau en 2) séparées par une valeur pivot. Comme nous divisons à chaque fois le problème en 2, nous parlons d'algorithme dichotomique.
Le même principe est appliqué à chaque patrie. Nous pouvons donc en déduire que nous utiliserons un procédé récursif pour le tri rapide.
Le principe comporte certaines similarités avec le tri par fusion, mais ici les deux sous-structures n'ont pas nécessairement une taille semblable (car c'est le pivot qui détermine l'endoit de la séparation), et pour le tri rapide il n'est pas nécessaire de fusionner les sous ensembles lors de la remontée dans la pile de récursion.
Le choix du pivot est relativement important, et en pratique nous pouvons utiliser le premier ou le dernier élément.
Merge Sort : Tri par fusions
Comme pour le tri rapide, le tri par fusions repose sur le principe "diviser pour régner" (divide and conquer). Nous pouvons simplifier le tri en divisant notre structure en structures plus petites de même dimension à une valeur près (par exemple diviser notre tableau en 2 parties). Comme nous divisons à chaque fois le problème en 2, nous parlons d'algorithme dichotomique.
Le même principe est appliqué à chaque patrie. Nous pouvons donc en déduire que nous utiliserons un procédé récursif pour le tri par fusions.
lorsque nous ne pouvons plus diviser notre sous-tableau (une seule cellule), la récursion s'arrête, et nous remontons la pile de récursion en fusionnant à chaque fois les sous-structures, jusqu'au moment où nous atteignons le niveau de départ et que notre structure est triée.
Complexité du tri par fusions
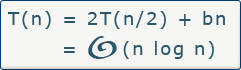
Nous pouvons constater que la complexité du tri par fusion ![]() (n log n) est nettement inférieure à la complexité du tri par sélections
(n log n) est nettement inférieure à la complexité du tri par sélections ![]() (n2). Le tri par fusions est beaucoup plus rapide que le tri par sélections.
(n2). Le tri par fusions est beaucoup plus rapide que le tri par sélections.
Exemple de code Pascal de tri par fusions
Code Pascal (Tri par fusion) (17 lignes)
Version en cache
04/10/2025 11:57:33 Cette version de la page est en cache (à la date du 04/10/2025 11:57:33) afin d'accélérer le traitement.Vous pouvez activer le mode utilisateur dans le menu en haut pour afficher la version plus récente de la page.
Document créé le 16/06/2005, dernière modification le 26/10/2018
Source du document imprimé : https://www.gaudry.be/programmer-trier.html
L'infobrol est un site personnel dont le contenu n'engage que moi. Le texte est mis à disposition sous licence CreativeCommons(BY-NC-SA). Plus d'info sur les conditions d'utilisation et sur l'auteur.


