Les algorithmes des arbres

Table des matières

Exemple d'arbre:

Arbre informatique

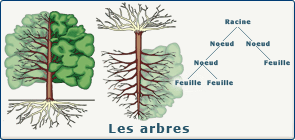
Le problème est le suivant: comment parcourir tous les points de l'arbre?

Dans le cas de notre arbre, deux possibilités maximum s'offrent à nous à chaque point (nous parlerons donc d'arbre binaire).

Partons du principe que nous nous trouvons en cours de programme, et que nous sommes donc sur un des points.

Trois possibilités d'actions s'offrent à nous:

  • Nous nous dirigeons vers la branche de gauche si elle existe (G).
  • Nous nous dirigeons vers la branche de droite si elle existe (D).
  • Nous traitons la valeur courante (T).

Nous pouvons arranger ces actions de différentes manières, mais retenons la position du traitement de la valeur courante (T).
Ce traitement peut se faire à trois moments:

  • Avant toute décision de direction (ex: TGD). Nous parlerons de traitement préfixe.
  • Après la première décision (ex: GTD). Nous parlerons de traitement infixe.
  • Après toute décision de direction (ex: GDT). Nous parlerons de traitement postfixe.

Comme nous pouvons définir chaque point de notre arbre comme étant un arbre avec ou sans arbre à chaque branche, nous remarquons l'effet récursif de ce type, ce qui nous amènera à un programme très compact et puissant.

Table des matières Haut

Code des arbres en  C

Ne nous occupons pas maintenant du code qui permet de définir les valeurs de l'arbre... ce qui nous intéresse à ce stade est la manière de parcourir les éléments.

Le programme ParcoursI.c nous propose une fonction ParcoursI, qui visite l'arbre et renvoie de manière incursive les valeurs du champ info par le canal de sortie standard.

  1. #include <stdio.h>
  2.  
  3. typedef struct blocA *Pt;
  4. typedef struct blocA
  5. {
  6. 	int info;
  7. 	Pt gauche;
  8. 	Pt droite;
  9. }
  10. Elem;
  11.  
  12. void ParcoursI (Pt p)
  13. {
  14. 	if (p!=NULL)
  15. 	{
  16. 		ParcoursI(p->gauche); printf ("%d", p->info);
  17. 		ParcoursI(p->droite);
  18. 	}
  19. }
  20.  
  21. void main (void)
  22. {
  23. 	Pt rac; /*Racine*/
  24. 	//... suite du programme ...
  25. 	ParcoursI(rac)
  26. }

Version en cache

18/12/2024 16:53:58 Cette version de la page est en cache (à la date du 18/12/2024 16:53:58) afin d'accélérer le traitement. Vous pouvez activer le mode utilisateur dans le menu en haut pour afficher la dernère version de la page.

Document créé le 06/11/2003, dernière modification le 26/10/2018
Source du document imprimé : https://www.gaudry.be/c-tree-algorithm.html

L'infobrol est un site personnel dont le contenu n'engage que moi. Le texte est mis à disposition sous licence CreativeCommons(BY-NC-SA). Plus d'info sur les conditions d'utilisation et sur l'auteur.