Exemple d'algorithme DFS

Légende & situation

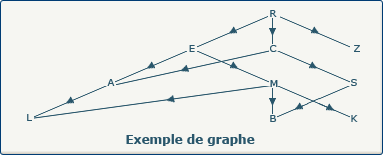
Graphe de départ. Ce graphe est celui que nous avons utilisé lorsque nous avons vu l'algorithme DFS, mais ici les étiquettes des sommets portent des lettres aléatoires au lieu de chiffres afin d'éviter toute confusion.

[Étape 0-0]  Initialisation des valeurs

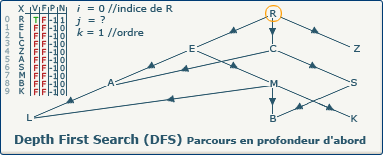
Nous utilisons ici les mêmes variables que lors des explications sur l'algorithme DFS, mais comme la place manquait sur les images, une seule lettre sera utilisée pour les variables :

• Tableaux 
  • X représente l'ensemble des sommets du graphe.
    La première colonne de l'illustration ci-dessus représente les indices dans X, et la deuxième colonne représente les sommets à ces indices dans X.
  • V (visitedVertices) représente le tableau de booléens qui permet de savoir si un sommet à déjà été visité ou pas.
  • F (closedVertices) représente le tableau de booléens qui permet de savoir si un sommet est fermé ou pas.
  • P (previousVertices) représente le tableau qui permet de retrouver le sommet précédent par lequel ce sommet à été découvert.
  • N (verticesOrders) représente le tableau qui permet de retrouver l'ordre d'exploration des sommets.
• Variables scalaires 
  • k est le compteur qui permet de donner un numéro d'ordre d'exploration aux sommets.
  • i et j sont les compteurs utilisé lors des itérations.

Comme nous démarrons avec le sommet R, nous le considérons comme visité (voir colonne V), et son numéro d'ordre d'exploration est 1.

[Étape 1-0]  Découverte du sommet E

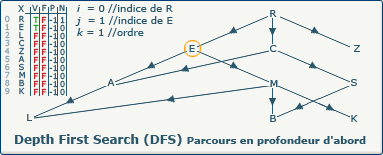
Nous sommes dans la boucle si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

L'exploration DFS découvre le sommet E. Nous affectons la valeur 1 (indice du sommet E dans le tableau X) à la variable j

visitedVertices[j] := true; devient visitedVertices[1] := true; afin de marquer le sommet E comme "visité".

Contents Haut

[Étape 1-1]  Incrémentation du compteur k (2)

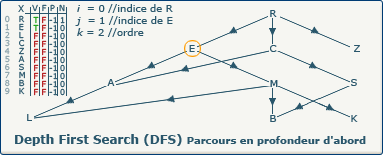
k := k+1; devient k := 1+1;.

Nous devons incrémenter le compteur k (ordre d'exploration) qui possède donc à présent la valeur 2 car un nouveau sommet (E) a été découvert.

[Étape 1-2]  Affectation du numéro d'exploration 2

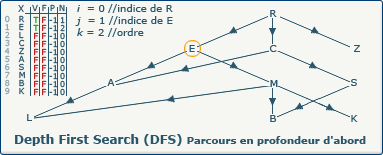
verticesOrders[j] := k; devient verticesOrders[1] := 2;

Nous utilisons la valeur du compteur k (2) pour affecter au sommet E son ordre d'exploration dans le tableau N à l'indice 1.

[Étape 1-3]  Affectation du précédent pour E

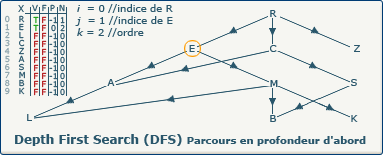
previousVertices[j] := i; devient previousVertices[1] := 0;

Nous affectons pour le tableau P à l'indice 1 l'indice du sommet précédent. C'est depuis ce sommet que E a été découvert.

[Étape 1-4]  i := j

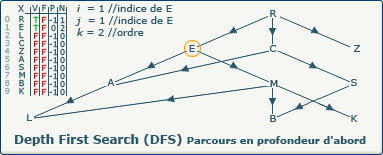
i := j; devient i := 1;.

Comme nous allons continuer notre exploration, nous devons nous souvenir du chemin emprunté.

Cela est possible en affectant la valeur de j (1) à la variable i (anciennement 0).

[Étape 2-0]  Découverte du sommet A

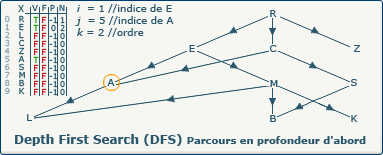
Nous sommes dans la boucle si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

L'exploration DFS découvre le sommet A. Nous affectons la valeur 5 (indice du sommet A dans le tableau X) à la variable j

visitedVertices[j] := true; devient visitedVertices[5] := true; afin de marquer le sommet A comme "visité".

Contents Haut

[Étape 2-1]  Incrémentation du compteur k (3)

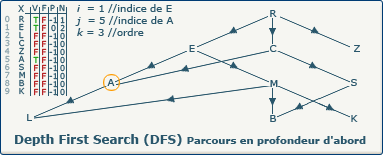
k := k+1; devient k := 2+1;.

Nous devons incrémenter le compteur k (ordre d'exploration) qui possède donc à présent la valeur 3 car un nouveau sommet (A) a été découvert.

[Étape 2-2]  Affectation du numéro d'exploration 3

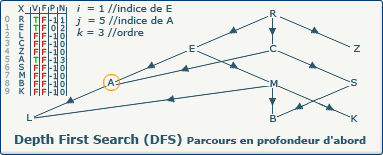
verticesOrders[j] := k; devient verticesOrders[5] := 3;

Nous utilisons la valeur du compteur k (3) pour affecter au sommet A son ordre d'exploration dans le tableau N à l'indice 5.

[Étape 2-3]  Affectation du précédent pour A

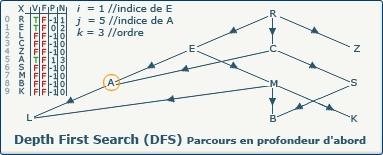
previousVertices[j] := i; devient previousVertices[5] := 1;

Nous affectons pour le tableau P à l'indice 5 l'indice du sommet précédent. C'est depuis ce sommet que A a été découvert.

[Étape 2-4]  i := j

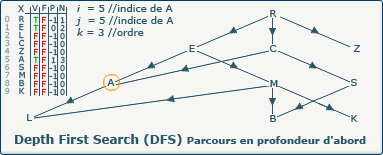
i := j; devient i := 5;.

Comme nous allons continuer notre exploration, nous devons nous souvenir du chemin emprunté.

Cela est possible en affectant la valeur de j (5) à la variable i (anciennement 1).

[Étape 3-0]  Découverte du sommet L

Nous sommes dans la boucle si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

L'exploration DFS découvre le sommet L. Nous affectons la valeur 2 (indice du sommet L dans le tableau X) à la variable j

visitedVertices[j] := true; devient visitedVertices[2] := true; afin de marquer le sommet L comme "visité".

Contents Haut

[Étape 3-1]  Incrémentation du compteur k (4)

k := k+1; devient k := 3+1;.

Nous devons incrémenter le compteur k (ordre d'exploration) qui possède donc à présent la valeur 4 car un nouveau sommet (L) a été découvert.

[Étape 3-2]  Affectation du numéro d'exploration 4

verticesOrders[j] := k; devient verticesOrders[2] := 4;

Nous utilisons la valeur du compteur k (4) pour affecter au sommet L son ordre d'exploration dans le tableau N à l'indice 2.

[Étape 3-3]  Affectation du précédent pour L

previousVertices[j] := i; devient previousVertices[2] := 5;

Nous affectons pour le tableau P à l'indice 2 l'indice du sommet précédent. C'est depuis ce sommet que L a été découvert.

[Étape 3-4]  i := j

i := j; devient i := 2;.

Comme nous allons continuer notre exploration, nous devons nous souvenir du chemin emprunté.

Cela est possible en affectant la valeur de j (2) à la variable i (anciennement 5).

[Étape 4-0]  Fermeture du sommet L

si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

Ce test de boucle échoue car il ne reste plus de sommet non visité qui soit suivant de L. Nous devons donc "fermer" ce dernier en affectant la valeur true dans le tableau F à l'indice 2.

closedVertices[i] := true; devient closedVertices[2] := true;

Contents Haut

[Étape 5-0]  Backtrack depuis le sommet L vers A

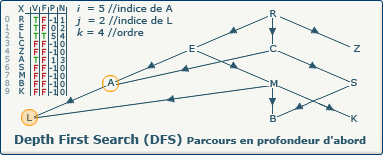
La variable i a été modifiée, et nous sommes entrés une nouvelle fois dans la boucle tant_que i > -1 faire...

La condition si closedVertices[2] = false, alors n'est pas respectée, le sommet courant (L) est fermé (valeur true dans le tableau F à l'indice 2), nous affectons à i la valeur du sommet précédent de L (A à l'indice 5)

i := previousVertices[i] devient i := 5

Contents Haut

[Étape 6-0]  Fermeture du sommet A

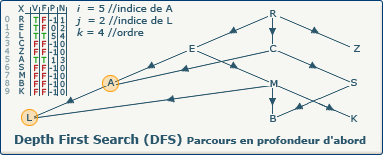
si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

Ce test de boucle échoue car il ne reste plus de sommet non visité qui soit suivant de A. Nous devons donc "fermer" ce dernier en affectant la valeur true dans le tableau F à l'indice 5.

closedVertices[i] := true; devient closedVertices[5] := true;

Contents Haut

[Étape 7-0]  Backtrack depuis le sommet A vers E

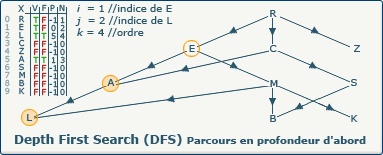
La variable i a été modifiée, et nous sommes entrés une nouvelle fois dans la boucle tant_que i > -1 faire...

La condition si closedVertices[5] = false, alors n'est pas respectée, le sommet courant (A) est fermé (valeur true dans le tableau F à l'indice 5), nous affectons à i la valeur du sommet précédent de A (E à l'indice 1)

i := previousVertices[i] devient i := 1

Contents Haut

[Étape 8-0]  Découverte du sommet M

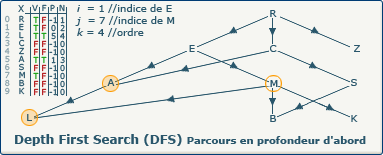
Nous sommes dans la boucle si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

L'exploration DFS découvre le sommet M. Nous affectons la valeur 7 (indice du sommet M dans le tableau X) à la variable j

visitedVertices[j] := true; devient visitedVertices[7] := true; afin de marquer le sommet M comme "visité".

Contents Haut

[Étape 8-1]  Incrémentation du compteur k (5)

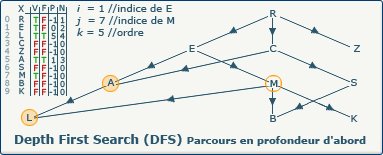
k := k+1; devient k := 4+1;.

Nous devons incrémenter le compteur k (ordre d'exploration) qui possède donc à présent la valeur 5 car un nouveau sommet (M) a été découvert.

[Étape 8-2]  Affectation du numéro d'exploration 5

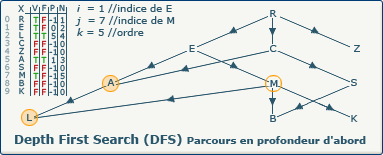
verticesOrders[j] := k; devient verticesOrders[7] := 5;

Nous utilisons la valeur du compteur k (5) pour affecter au sommet M son ordre d'exploration dans le tableau N à l'indice 7.

[Étape 8-3]  Affectation du précédent pour M

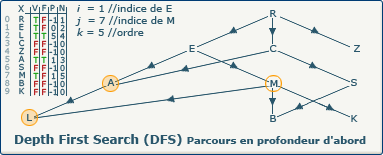
previousVertices[j] := i; devient previousVertices[7] := 1;

Nous affectons pour le tableau P à l'indice 7 l'indice du sommet précédent. C'est depuis ce sommet que M a été découvert.

[Étape 8-4]  i := j

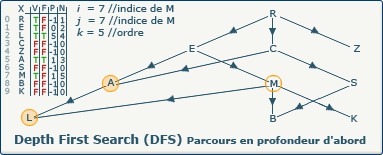
i := j; devient i := 7;.

Comme nous allons continuer notre exploration, nous devons nous souvenir du chemin emprunté.

Cela est possible en affectant la valeur de j (7) à la variable i (anciennement 1).

[Étape 9-0]  Découverte du sommet B

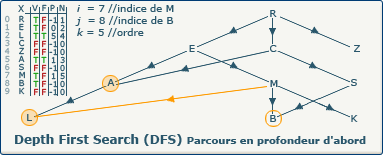
Nous sommes dans la boucle si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

L'exploration DFS découvre le sommet B. Nous affectons la valeur 8 (indice du sommet B dans le tableau X) à la variable j

visitedVertices[j] := true; devient visitedVertices[8] := true; afin de marquer le sommet B comme "visité".

Contents Haut

[Étape 9-1]  Incrémentation du compteur k (6)

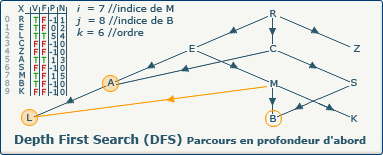
k := k+1; devient k := 5+1;.

Nous devons incrémenter le compteur k (ordre d'exploration) qui possède donc à présent la valeur 6 car un nouveau sommet (B) a été découvert.

[Étape 9-2]  Affectation du numéro d'exploration 6

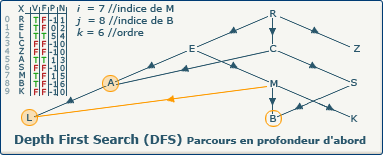
verticesOrders[j] := k; devient verticesOrders[8] := 6;

Nous utilisons la valeur du compteur k (6) pour affecter au sommet B son ordre d'exploration dans le tableau N à l'indice 8.

[Étape 9-3]  Affectation du précédent pour B

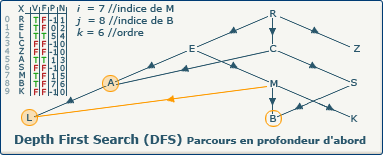
previousVertices[j] := i; devient previousVertices[8] := 7;

Nous affectons pour le tableau P à l'indice 8 l'indice du sommet précédent. C'est depuis ce sommet que B a été découvert.

[Étape 9-4]  i := j

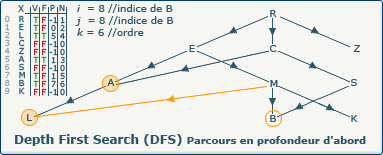
i := j; devient i := 8;.

Comme nous allons continuer notre exploration, nous devons nous souvenir du chemin emprunté.

Cela est possible en affectant la valeur de j (8) à la variable i (anciennement 7).

[Étape 10-0]  Fermeture du sommet B

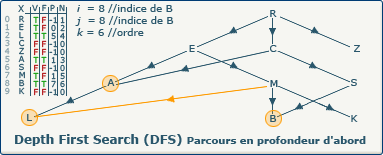
si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

Ce test de boucle échoue car il ne reste plus de sommet non visité qui soit suivant de B. Nous devons donc "fermer" ce dernier en affectant la valeur true dans le tableau F à l'indice 8.

closedVertices[i] := true; devient closedVertices[8] := true;

Contents Haut

[Étape 11-0]  Backtrack depuis le sommet B vers M

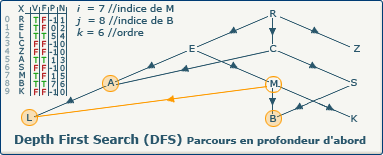
La variable i a été modifiée, et nous sommes entrés une nouvelle fois dans la boucle tant_que i > -1 faire...

La condition si closedVertices[8] = false, alors n'est pas respectée, le sommet courant (B) est fermé (valeur true dans le tableau F à l'indice 8), nous affectons à i la valeur du sommet précédent de B (M à l'indice 7)

i := previousVertices[i] devient i := 7

Contents Haut

[Étape 12-0]  Découverte du sommet K

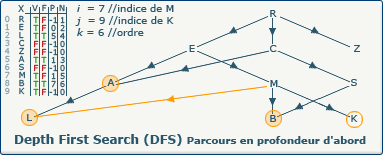
Nous sommes dans la boucle si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

L'exploration DFS découvre le sommet K. Nous affectons la valeur 9 (indice du sommet K dans le tableau X) à la variable j

visitedVertices[j] := true; devient visitedVertices[9] := true; afin de marquer le sommet K comme "visité".

Contents Haut

[Étape 12-1]  Incrémentation du compteur k (7)

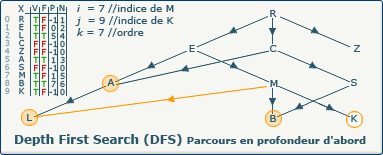
k := k+1; devient k := 6+1;.

Nous devons incrémenter le compteur k (ordre d'exploration) qui possède donc à présent la valeur 7 car un nouveau sommet (K) a été découvert.

[Étape 12-2]  Affectation du numéro d'exploration 7

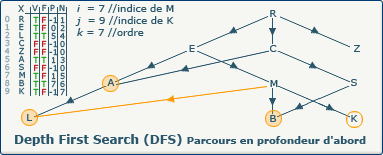
verticesOrders[j] := k; devient verticesOrders[9] := 7;

Nous utilisons la valeur du compteur k (7) pour affecter au sommet K son ordre d'exploration dans le tableau N à l'indice 9.

[Étape 12-3]  Affectation du précédent pour K

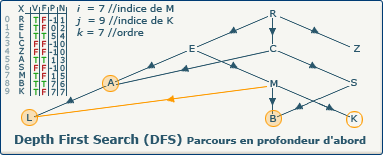
previousVertices[j] := i; devient previousVertices[9] := 7;

Nous affectons pour le tableau P à l'indice 9 l'indice du sommet précédent. C'est depuis ce sommet que K a été découvert.

[Étape 12-4]  i := j

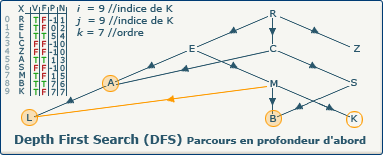
i := j; devient i := 9;.

Comme nous allons continuer notre exploration, nous devons nous souvenir du chemin emprunté.

Cela est possible en affectant la valeur de j (9) à la variable i (anciennement 7).

[Étape 13-0]  Fermeture du sommet K

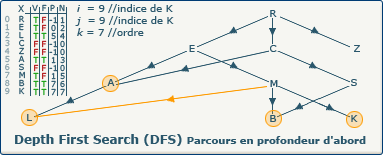
si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

Ce test de boucle échoue car il ne reste plus de sommet non visité qui soit suivant de K. Nous devons donc "fermer" ce dernier en affectant la valeur true dans le tableau F à l'indice 9.

closedVertices[i] := true; devient closedVertices[9] := true;

Contents Haut

[Étape 14-0]  Backtrack depuis le sommet K vers M

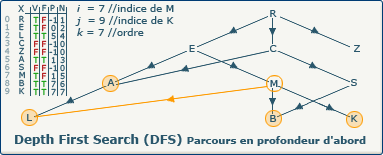
La variable i a été modifiée, et nous sommes entrés une nouvelle fois dans la boucle tant_que i > -1 faire...

La condition si closedVertices[9] = false, alors n'est pas respectée, le sommet courant (K) est fermé (valeur true dans le tableau F à l'indice 9), nous affectons à i la valeur du sommet précédent de K (M à l'indice 7)

i := previousVertices[i] devient i := 7

Contents Haut

[Étape 15-0]  Fermeture du sommet M

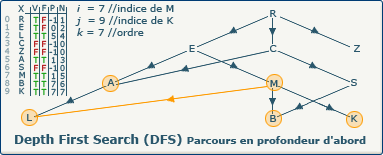
si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

Ce test de boucle échoue car il ne reste plus de sommet non visité qui soit suivant de M. Nous devons donc "fermer" ce dernier en affectant la valeur true dans le tableau F à l'indice 7.

closedVertices[i] := true; devient closedVertices[7] := true;

Contents Haut

[Étape 16-0]  Backtrack depuis le sommet M vers E

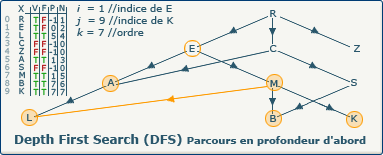
La variable i a été modifiée, et nous sommes entrés une nouvelle fois dans la boucle tant_que i > -1 faire...

La condition si closedVertices[7] = false, alors n'est pas respectée, le sommet courant (M) est fermé (valeur true dans le tableau F à l'indice 7), nous affectons à i la valeur du sommet précédent de M (E à l'indice 1)

i := previousVertices[i] devient i := 1

Contents Haut

[Étape 17-0]  Fermeture du sommet E

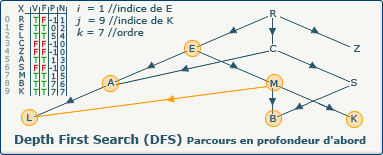
si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

Ce test de boucle échoue car il ne reste plus de sommet non visité qui soit suivant de E. Nous devons donc "fermer" ce dernier en affectant la valeur true dans le tableau F à l'indice 1.

closedVertices[i] := true; devient closedVertices[1] := true;

Contents Haut

[Étape 18-0]  Backtrack depuis le sommet E vers R

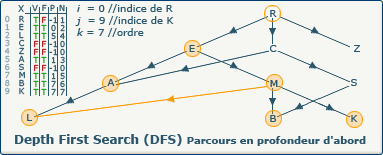
La variable i a été modifiée, et nous sommes entrés une nouvelle fois dans la boucle tant_que i > -1 faire...

La condition si closedVertices[1] = false, alors n'est pas respectée, le sommet courant (E) est fermé (valeur true dans le tableau F à l'indice 1), nous affectons à i la valeur du sommet précédent de E (R à l'indice 0)

i := previousVertices[i] devient i := 0

Contents Haut

[Étape 19-0]  Découverte du sommet C

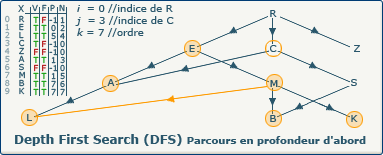
Nous sommes dans la boucle si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

L'exploration DFS découvre le sommet C. Nous affectons la valeur 3 (indice du sommet C dans le tableau X) à la variable j

visitedVertices[j] := true; devient visitedVertices[3] := true; afin de marquer le sommet C comme "visité".

Contents Haut

[Étape 19-1]  Incrémentation du compteur k (8)

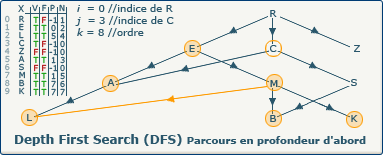
k := k+1; devient k := 7+1;.

Nous devons incrémenter le compteur k (ordre d'exploration) qui possède donc à présent la valeur 8 car un nouveau sommet (C) a été découvert.

[Étape 19-2]  Affectation du numéro d'exploration 8

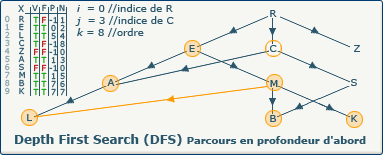
verticesOrders[j] := k; devient verticesOrders[3] := 8;

Nous utilisons la valeur du compteur k (8) pour affecter au sommet C son ordre d'exploration dans le tableau N à l'indice 3.

[Étape 19-3]  Affectation du précédent pour C

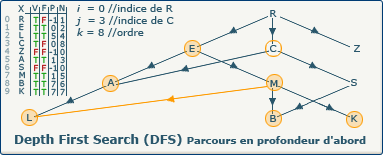
previousVertices[j] := i; devient previousVertices[3] := 0;

Nous affectons pour le tableau P à l'indice 3 l'indice du sommet précédent. C'est depuis ce sommet que C a été découvert.

[Étape 19-4]  i := j

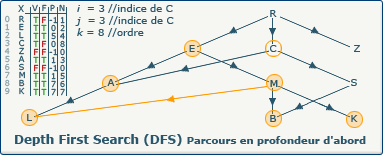
i := j; devient i := 3;.

Comme nous allons continuer notre exploration, nous devons nous souvenir du chemin emprunté.

Cela est possible en affectant la valeur de j (3) à la variable i (anciennement 0).

[Étape 20-0]  Découverte du sommet S

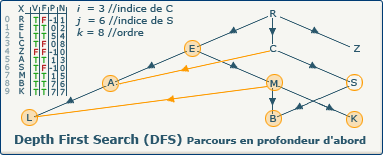
Nous sommes dans la boucle si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

L'exploration DFS découvre le sommet S. Nous affectons la valeur 6 (indice du sommet S dans le tableau X) à la variable j

visitedVertices[j] := true; devient visitedVertices[6] := true; afin de marquer le sommet S comme "visité".

Contents Haut

[Étape 20-1]  Incrémentation du compteur k (9)

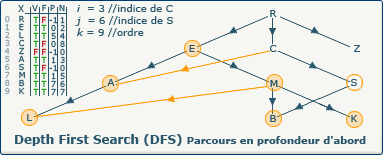
k := k+1; devient k := 8+1;.

Nous devons incrémenter le compteur k (ordre d'exploration) qui possède donc à présent la valeur 9 car un nouveau sommet (S) a été découvert.

[Étape 20-2]  Affectation du numéro d'exploration 9

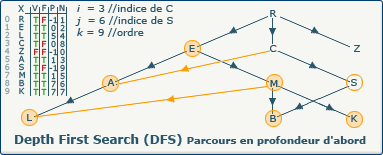
verticesOrders[j] := k; devient verticesOrders[6] := 9;

Nous utilisons la valeur du compteur k (9) pour affecter au sommet S son ordre d'exploration dans le tableau N à l'indice 6.

[Étape 20-3]  Affectation du précédent pour S

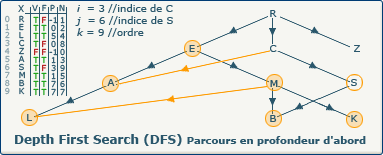
previousVertices[j] := i; devient previousVertices[6] := 3;

Nous affectons pour le tableau P à l'indice 6 l'indice du sommet précédent. C'est depuis ce sommet que S a été découvert.

[Étape 20-4]  i := j

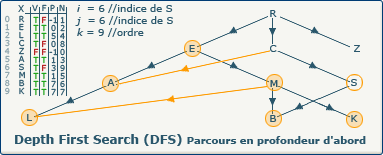
i := j; devient i := 6;.

Comme nous allons continuer notre exploration, nous devons nous souvenir du chemin emprunté.

Cela est possible en affectant la valeur de j (6) à la variable i (anciennement 3).

[Étape 21-0]  Fermeture du sommet S

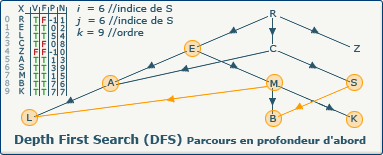
si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

Ce test de boucle échoue car il ne reste plus de sommet non visité qui soit suivant de S. Nous devons donc "fermer" ce dernier en affectant la valeur true dans le tableau F à l'indice 6.

closedVertices[i] := true; devient closedVertices[6] := true;

Contents Haut

[Étape 22-0]  Backtrack depuis le sommet S vers C

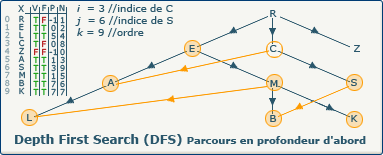
La variable i a été modifiée, et nous sommes entrés une nouvelle fois dans la boucle tant_que i > -1 faire...

La condition si closedVertices[6] = false, alors n'est pas respectée, le sommet courant (S) est fermé (valeur true dans le tableau F à l'indice 6), nous affectons à i la valeur du sommet précédent de S (C à l'indice 3)

i := previousVertices[i] devient i := 3

Contents Haut

[Étape 23-0]  Fermeture du sommet C

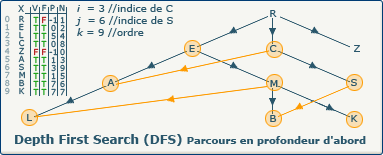
si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

Ce test de boucle échoue car il ne reste plus de sommet non visité qui soit suivant de C. Nous devons donc "fermer" ce dernier en affectant la valeur true dans le tableau F à l'indice 3.

closedVertices[i] := true; devient closedVertices[3] := true;

Contents Haut

[Étape 24-0]  Backtrack depuis le sommet C vers R

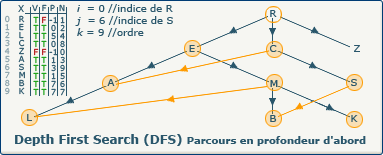
La variable i a été modifiée, et nous sommes entrés une nouvelle fois dans la boucle tant_que i > -1 faire...

La condition si closedVertices[3] = false, alors n'est pas respectée, le sommet courant (C) est fermé (valeur true dans le tableau F à l'indice 3), nous affectons à i la valeur du sommet précédent de C (R à l'indice 0)

i := previousVertices[i] devient i := 0

Contents Haut

[Étape 25-0]  Découverte du sommet Z

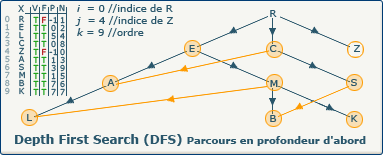
Nous sommes dans la boucle si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

L'exploration DFS découvre le sommet Z. Nous affectons la valeur 4 (indice du sommet Z dans le tableau X) à la variable j

visitedVertices[j] := true; devient visitedVertices[4] := true; afin de marquer le sommet Z comme "visité".

Contents Haut

[Étape 25-1]  Incrémentation du compteur k (10)

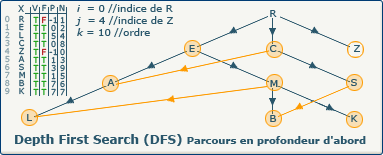
k := k+1; devient k := 9+1;.

Nous devons incrémenter le compteur k (ordre d'exploration) qui possède donc à présent la valeur 10 car un nouveau sommet (Z) a été découvert.

[Étape 25-2]  Affectation du numéro d'exploration 10

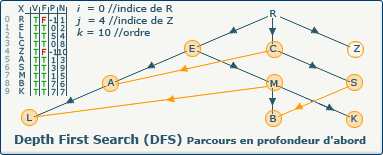
verticesOrders[j] := k; devient verticesOrders[4] := 10;

Nous utilisons la valeur du compteur k (10) pour affecter au sommet Z son ordre d'exploration dans le tableau N à l'indice 4.

[Étape 25-3]  Affectation du précédent pour Z

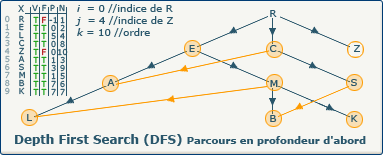
previousVertices[j] := i; devient previousVertices[4] := 0;

Nous affectons pour le tableau P à l'indice 4 l'indice du sommet précédent. C'est depuis ce sommet que Z a été découvert.

[Étape 25-4]  i := j

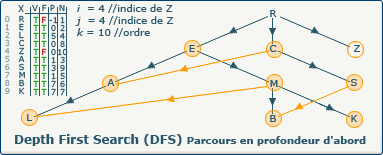
i := j; devient i := 4;.

Comme nous allons continuer notre exploration, nous devons nous souvenir du chemin emprunté.

Cela est possible en affectant la valeur de j (4) à la variable i (anciennement 0).

[Étape 26-0]  Fermeture du sommet Z

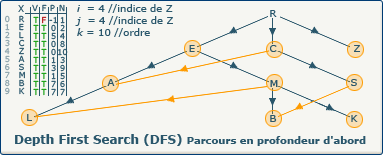
si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

Ce test de boucle échoue car il ne reste plus de sommet non visité qui soit suivant de Z. Nous devons donc "fermer" ce dernier en affectant la valeur true dans le tableau F à l'indice 4.

closedVertices[i] := true; devient closedVertices[4] := true;

Contents Haut

[Étape 27-0]  Backtrack depuis le sommet Z vers R

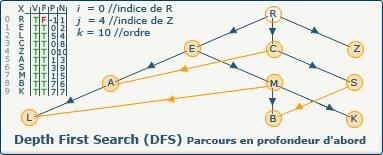
La variable i a été modifiée, et nous sommes entrés une nouvelle fois dans la boucle tant_que i > -1 faire...

La condition si closedVertices[4] = false, alors n'est pas respectée, le sommet courant (Z) est fermé (valeur true dans le tableau F à l'indice 4), nous affectons à i la valeur du sommet précédent de Z (R à l'indice 0)

i := previousVertices[i] devient i := 0

Contents Haut

[Étape 28-0]  Fermeture du sommet R

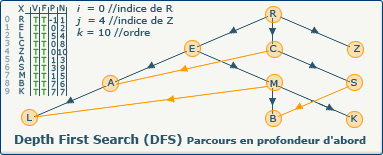
si ∃ y : (x,y) ∈ A ∧ visitedVertices[j]=false

Ce test de boucle échoue car il ne reste plus de sommet non visité qui soit suivant de R. Nous devons donc "fermer" ce dernier en affectant la valeur true dans le tableau F à l'indice 0.

closedVertices[i] := true; devient closedVertices[0] := true;

Contents Haut

[Étape 29-0]  Non-respect de la condition de boucle

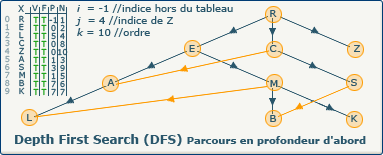
L'algorithme prend effectivement fin avant d'entrer dans la boucle tant_que i > -1 faire..., car la condition n'est pas respectée :-1 (indice du précédent de R) n'est pas > que -1 (nous testons avec le plus petit index du tableau moins un, donc -1 dans le cas d'un langage pour lequel le premier indice d'un tableau est 0).

Ordre d'exploration DFS

U bevindt zich op de Engels versie van de site, maar uw systeem geeft aan dat u liever de Nederlandse taal gebruikt.
De hele site is nog niet vertaald, maar de menu's en knoppen op de interface zijn grotendeels vertaald.

Wilt u de pagina in het Nederlands bereiken?
Klik hier om door te gaan in het Nederlands: Raadpleeg de Nederlandse versie van deze pagina

Sie befinden sich in der Englisch Version der Website, Ihr System gibt jedoch an, dass Sie die deutsche Sprache bevorzugen.
Die gesamte Site ist noch nicht übersetzt, aber die Menüs und Schaltflächen auf der Benutzeroberfläche sind weitgehend übersetzt.

Möchten Sie die Seite auf Deutsch erreichen?
Klicken Sie hier, um fortzufahren: Konsultieren Sie die deutsche Version dieser Seite

Vous vous trouvez sur la version anglaise du site, mais votre système indique que vous préférez utiliser la langue française.

Souhaitez-vous atteindre la page en français?
Cliquez ici pour continuer en français: Consulter la page en français