Opérations sur les matrices
Egalité de matrices
Définition
Deux matrices A = (aij) et B = (bij) sont égales si
- elles sont de même format.
- aij = bij pour tout i et j.
Somme de deux matrices
Définition
Soit deux matrices A = (aij) et B = (bij), la somme des deux matrices est une matrice C = (cij)
- de même format.
- telle que cij = aij + bij pour tout i et j.
Exemple
Soit A et B les matrices suivantes :
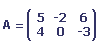
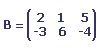
La somme des deux matrices est la matrice suivante :
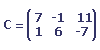
Remarque: l'addition est commutative (A+B=B+A).
Différence de deux matrices
Définition
Soit deux matrices A = (aij) et B = (bij), la différence des deux matrices est une matrice C = (cij)
- de même format.
- telle que cij = aij - bij pour tout i et j.
Exemple
Soit A et B les matrices suivantes :
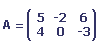
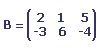
La différence des deux matrices est la matrice suivante :
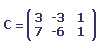
Remarques :
- La différence n'est pas commutative.
- A-B = -(B-A).
Produit d'une matrice par un scalaire
Définition
Soit une matrice quelconque A = (aij), et un scalaire ß, le produit des deux est une matrice B = (bij)
- de même format que A.
- telle que bij = ßaij pour tout i et j.
Exemple
Soit A la matrice suivantes:
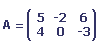
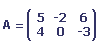
Le produit de la matrices et du scalaire 2 est la matrice suivante:
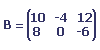
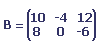
Produit de deux matrices
Définition
Soit deux matrices A = (aij) de format m*n, et B = (bij) de format n*p,
le produit des deux matrices est une matrice C = (cij)
- de format m*p.
- telle que cij est le produit de la ligne i de A par la colonne j de B pour tout i et j.
Exemple
Soit A et B les matrices suivantes:
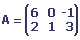
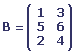
Le produit des deux matrices est la matrice suivante:
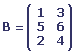
Remarque:
- Le produit matriciel n'est pas commutatif.
Deutsche Übersetzung
Sie haben gebeten, diese Seite auf Deutsch zu besuchen. Momentan ist nur die Oberfläche übersetzt, aber noch nicht der gesamte Inhalt.Wenn Sie mir bei Übersetzungen helfen wollen, ist Ihr Beitrag willkommen. Alles, was Sie tun müssen, ist, sich auf der Website zu registrieren und mir eine Nachricht zu schicken, in der Sie gebeten werden, Sie der Gruppe der Übersetzer hinzuzufügen, die Ihnen die Möglichkeit gibt, die gewünschten Seiten zu übersetzen. Ein Link am Ende jeder übersetzten Seite zeigt an, dass Sie der Übersetzer sind und einen Link zu Ihrem Profil haben.
Vielen Dank im Voraus.
Dokument erstellt 19/03/2002, zuletzt geändert 26/10/2018
Quelle des gedruckten Dokuments:https://www.gaudry.be/de/matrices-operations.html
Die Infobro ist eine persönliche Seite, deren Inhalt in meiner alleinigen Verantwortung liegt. Der Text ist unter der CreativeCommons-Lizenz (BY-NC-SA) verfügbar. Weitere Informationen auf die Nutzungsbedingungen und dem Autor.


