Analyse, Pert et le chemin critique
Dans le cadre de l’analyse d’un projet1, il est important de pouvoir rapidement déterminer combien de temps et dans quel ordre nous devrons effectuer les différentes tâches (les processus) qui composent notre projet.
Un exemple concret est la construction d’un bâtiment. Il est nécessaire d’ordonner les différents ouvrages des corps de métiers qui interviendront. Chaque ouvrage nécessite un temps minimum d’exécution (durée). Certains ouvrages nécessitent que d’autres ouvrages soient terminés (dépendance). Certains ouvrages peuvent durer plus longtemps, mais ceux dont dépendent d’autres ouvrages ne peuvent souffrir d’aucun retard sans impacter la date de fin du projet global.
Historique de la méthode Pert
En 1955, la marine américaine est chargée d’établir le système d’arme POLARIS (réaliser en même temps un sous-marin lanceur, et le missile balistique mer-sol contenant une tête nucléaire, lancé depuis le sous-marin en plongée), et souhaite rattraper son retard dans la course à la guerre des étoiles et la balistique stratégique (dû en partie à l’échec du programme Jupiter).
Afin de mesurer et prévoir l’état d’avancement des progrès du projet, un outil a donc été mis au point pour aider à la prise de décisions lors de la planification : PERT (Program evaluation and review technique). Il s’agit de rechercher un temps d’exécution minimum nécessaire à l’élaboration d’une tâche complexe (le projet POLARIS), divisée en sous-tâches élémentaires (ou processus) pour lesquelles des contraintes existent. Ces tâches se succèdent ou démarrent simultanément ; c’est donc un cas de gestion d’ordonnancement qui sera résolu par des graphes.
L’utilisation de PERT a permis de réduire la durée à 4 ans au lieu des 7 ans initialement prévus.
PERT, et son application graphique Gantt, sont des moyens d’aide à la prise de décision lors de la planification, mais PERT est légèrement moins efficace en termes de complexité que son dérivé français MPM (Méthode des Potentiels Metra), car ce dernier produit des graphes plus petits.
Principes d’ordonnancement de projet
Trois facteurs interviennent dans les problèmes d’ordonnancement :
- Le temps
- date de début au plus tôt : en fonction des processus dont dépend le processus visé
- date de début au plus tard : sinon la date de fin de l’ensemble du projet est retardée
- durée
- Les ressources (matériel, ressources humaines, etc.).
- Les contraintes techniques (dans le cas de notre exemple de bâtiment, les temps de séchage avant de passer à l’étape suivante).
Méthode PERT pour modéliser l’ordonnancement
Afin de modéliser le problème posé par l’ordonnancement de notre projet, ses contraintes, et déterminer le chemin critique (en terme de temps et de coût), nous pouvons utiliser la méthode PERT qui produira un graphe de telle manière que les arcs représentent les processus effectifs, pondérés par les durées, et les sommets représentent les successions de processus (et les deux processus fictifs).
La méthode MPM utilise une notation opposée (les tâches sont les sommets du graphe, et les successions entre les tâches sont les arcs du graphe).
Note : il existe deux processus fictifs (c’est-à-dire de durée nulle) : T0, qui correspond au début du projet (la racine), et Tn+1 qui correspond à la fin de tous les processus, et donc du projet (l’objectif).
Une étape dans PERT
Chaque étape de notre projet est un sommet valide dans le graphe PERT s’il répond aux trois critères suivants :
- être un moment important, mesurable
- Etre le départ ou la fin d’un processus
- Etre de durée nulle et ne nécessiter aucune ressource en sois
Le début et la fin du projet sont des étapes (ou processus fictifs), et donc représentés comme des sommets, qui ont en outre la particularité d’être le début et la fin du (ou des) chemin(s) critique(s).
Une tâche dans PERT
Chaque processus de notre projet est une opération qui sera un arc valide s’il répond aux critères suivants :
- Représenter le travail à accomplir pour passer d’une étape à l’autre (d’un sommet à l’autre)
- Etre de durée non nulle
Aucune étape ne peut être considérée comme atteinte tant que toutes les tâches qui y mènent ne sont pas terminées.
Aucune tâche ne peut être démarrée tant que son étape de départ n’est pas atteinte.
PERT de temps
Le temps intervient à différents niveaux dans PERT.
- Durée :
- La plus courte (quand tout se passe bien)
- La plus longue (quand tout se passe mal)
- La moyenne
- Dates : des PKI (Performance Key Indicator) peuvent jalonner le projet, et correspondent le plus souvent aux étapes.
- Date au plus tôt : quand les tâches dont dépend la tâche actuelle sont terminées.
- Date au plus tard : si cette date est dépassée, la date de fin du projet sera dépassée aussi. Il faut donc soustraire chaque processus (tâche) en remontant leur cours depuis la fin vers la tâche actuelle, et nous obtenons le temps maximal autorisé.
- Marge : la différence entre la date au plus tôt et la date au plus tard.
Avant d'aller plus loin, nous devons nous familiariser avec quelques abréviations que nous utiliserons lors de notre méthode Pert pour chaque tâche:
- EST [“Earliest Starting Time”2] : le moment le plus tôt ou nous pouvons démarrer une tâche.
- LST [“Latest Starting Time”4] : le moment le plus tard ou nous pouvons démarrer une tâche. Si nous démarrons la tâche après ce moment, nous ne pouvons garantir totalement que la date de fin du projet sera respectée.
- TS [“Total Slack”6] : le retard maximum que peut prendre le démarrage d'une tâche sans impacter la date de fin de projet. Il s'agit tout simplement du LST auquel on soustrait le EST.
- FS [“Free Slack”8] : le retard maximum que peut prendre le démarrage d'une tâche sans impacter les EST des tâches qui dépendent de cette tâche.
Exemple PERT
Nous pouvons appliquer ces principes à un exemple concret: la construction d'une route.
Définition des tâches pour PERT
Nous allons déterminer les différentes tâches à accomplir, sans nous tracasser de l'ordre dans lequel les effectuer, et nous allons leur affecter un identifiant (ici une lettre majuscule).
Calcul des durées pour PERT
Nous devons à présent estimer les durées que prendront normalement chaque tâche. Si nous n'avons aucune expérience dans ce genre de projet, nous devons nous entourer d'une équipe d'experts.
Après un tour de table, les différents intervenants nous ont fourni les estimations suivantes pour le coût en unité de temps pour effectuer une tâche X : 30, 10, 15, 20, 20, 30, 5, 10, 30, 5, 6, 10, 10.
Nous avons donc comme moyenne : 201/13=16 (on arrondit à la valeur entière supérieure).
Nous pouvons aussi calculer le delta selon la formule suivante :
D = [valeur minimale + (x * valeur moyenne) + valeur maximale] / (x + 1 + 1)
Si nous choisissons la valeur 4 pour x, notre calcul devient [5 + (4*16) + 30] / 6 = 17 (16.5 mais on arrondit à la valeur entière supérieure).
Appliquons à présent ce principe à notre exemple de route, pour calculer les durées des tâches...
Contraintes temporelles pour PERT
Après examen, nous nous rendons compte que la tâche B ne peut débuter que lorsque D est terminé. En effet, ce sont les terres qui résultent du décapage (D) que nous devons évacuer.
La tâche Y (Pose de panneaux de signalisation) ne dépend d'aucune autre tâche. Elle peut commencer au plus tôt au début du projet, et au plus tard la date de fin moins la durée nécessaire à l'accomplir.
Notre exemple est assez simple, et toutes les autres tâches dépendent en général de la tâche précédente.
Graphique PERT
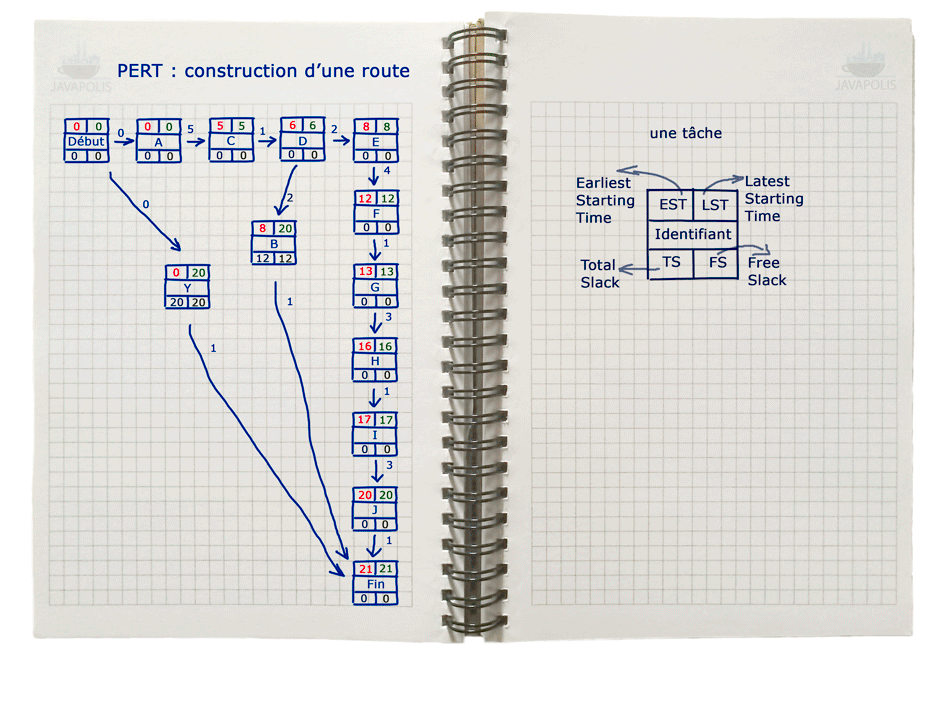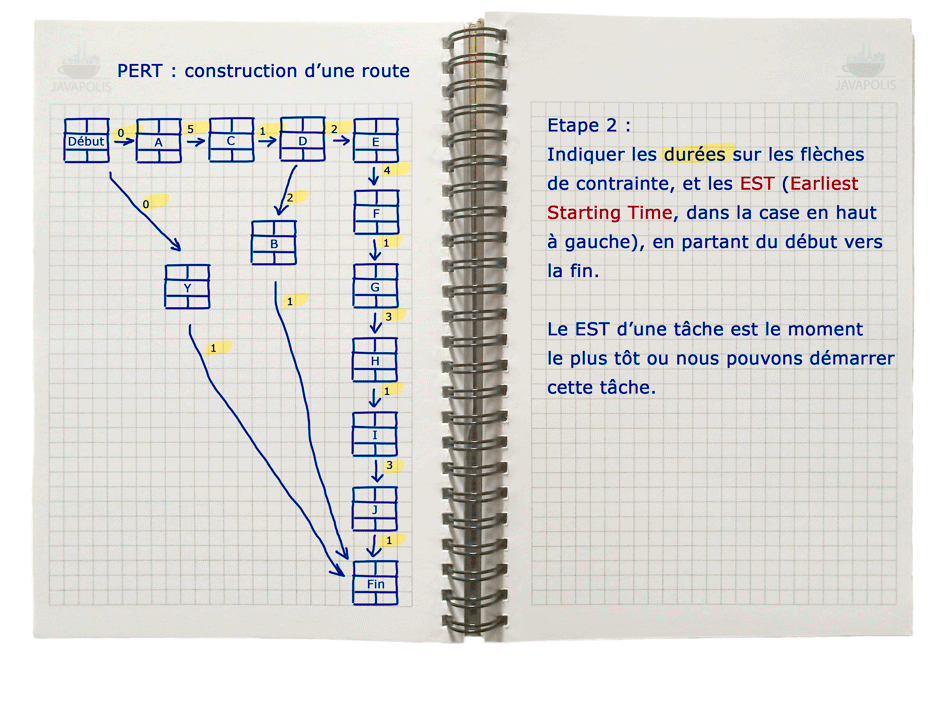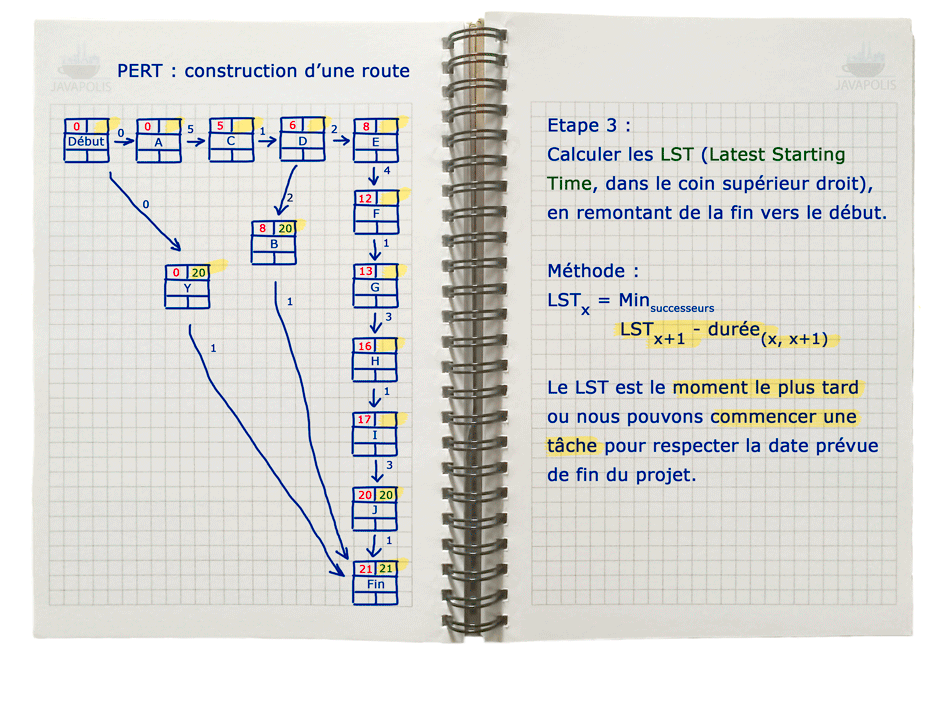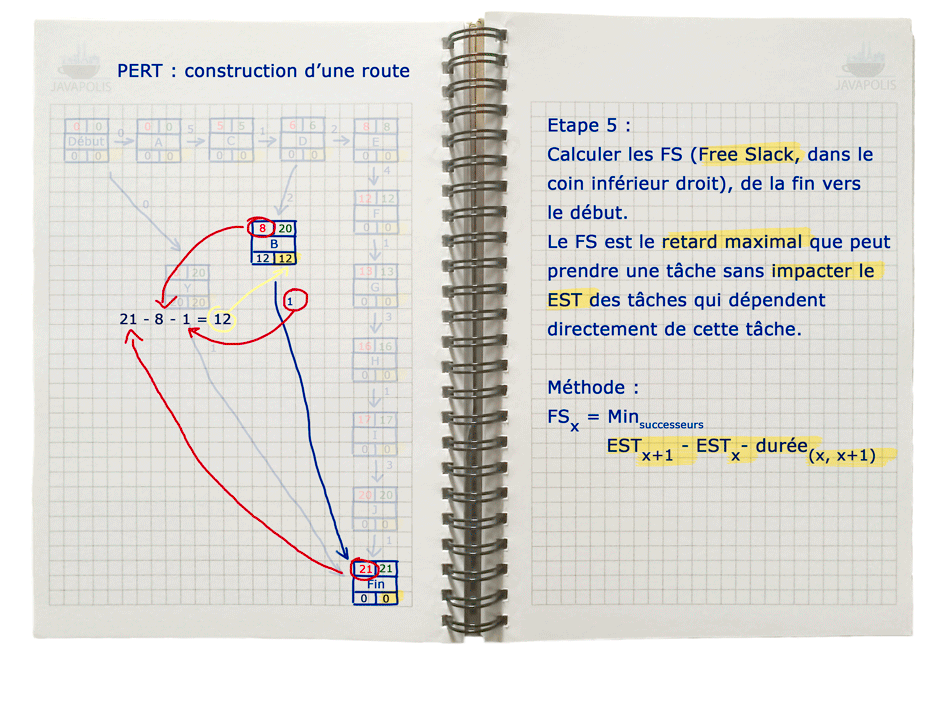
Cliquez sur l'image pour afficher l'animation en grand.
Version en cache
14/09/2025 12:01:11 Cette version de la page est en cache (à la date du 14/09/2025 12:01:11) afin d'accélérer le traitement.Vous pouvez activer le mode utilisateur dans le menu en haut pour afficher la version plus récente de la page.
Document créé le 24/12/2005, dernière modification le 28/10/2018
Source du document imprimé : https://www.gaudry.be/analyse-pert.html
L'infobrol est un site personnel dont le contenu n'engage que moi. Le texte est mis à disposition sous licence CreativeCommons(BY-NC-SA). Plus d'info sur les conditions d'utilisation et sur l'auteur.
- ↑ Gestion de projet : Il s'agit plus ici de gestion de projet que d'analyse proprement dite. Dans le cycle de vie d'un projet, nous sommes dans la plannification, et non plus dans la définition.


